Jugadores, Conjuntos Cero y Montañas Fractales
Henry y Thomas están lanzando una moneda apostando 1 dólar a cada resultado. Si sale cara, Henry gana un dólar de Thomas. Si sale cruz, Thomas gana un dólar de Henry. Por tanto, la ganancia neta de Henry en dólares es el número total de caras menos el número total de cruces.
Si definimos x(n) como la función de ganancia neta de Henry, esta vendrá determinado por el siguiente sistema dinámico:
x (n) = x (n) + 1, con una probabilidad p = ½
x (n) = x (n) – 1, con una probabilidad q = ½
Si os acordáis, ya vimos la gráfica de 10.000 lanzamientos de la moneda en el artículo anterior. Si repetimos este experimento varias veces usando la hoja de cálculo de ese artículo, podemos extraer algunas conclusiones:
- A pesar de que las probabilidades son iguales cada lanzamiento de la moneda, las ganancias o pérdidas pueden sumar una cantidad significativa. A pesar de que una cara una cruz son igualmente de probables, puede haber una serie de «rachas» que produzcan una gran pérdida tanto a Henry como a Thomas. Esto resulta importante para entender el problema de «ruina del jugador» que veremos más adelante.
- El conjunto de puntos donde x(n) vuelve a x(n) = 0 (es decir, los puntos en los que se igualan ganancias y pérdidas) se denominan conjunto cero del sistema. Usando n como nuestra medida del tiempo, vemos que los intervalos de tiempo entre cada punto del conjunto cero son independientes, pero forman grupos, al igual que sucedía en el polvo de Cantor.
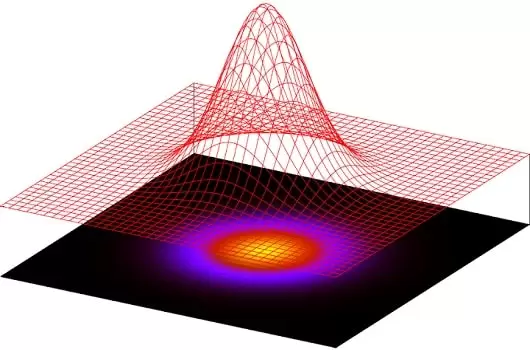
- Las fluctuaciones en las ganancias de Henry forman una gráfica que sugiere valles y montañas. De hecho, este es un tipo de «paisaje» browniano que vemos a nuestro alrededor todo el tiempo. Para crear diferentes paisajes «extraterrestres» basta con cambiar las probabilidades. Los efectos en 3D, con un poco de sombreado de color, puede ser impresionantes.
Dado que más adelante vamos a ver movimientos que no son Brownianos, y distribuciones que no son Normales, es importante primero que veamos un aspecto que es independiente de la distribución de probabilidad. Es el denominado problema de ruina del jugador. No es necesario utilizar distribuciones no Normales para arruinar a un jugador: con una Normal también nos va bien.
La Operativa en Futuros y el Problema de Ruina del Jugador
En este apartado vamos a ver cómo los casinos ganan la mayor parte de su dinero, así como por qué los traders de Goldman Sachs ganan más dinero especulando que nosotros. El motivo no tiene por qué ser necesariamente que sean más inteligentes. En realidad es porque tienen más dinero (aunque también vamos a mostrar cómo los que tienen dinero también pueden perder fácilmente esta ventaja).
Mucha gente asume que el precio de los futuros sobre índices, bonos, divisas o materias primas representa una apuesta justa. Es decir, suponen que la probabilidad de un movimiento al alza en el precio de futuros es igual que la probabilidad de un movimiento a la baja, y por lo tanto la esperanza matemática de una ganancia o pérdida es cero. Utilizan la analogía de tirar una moneda al aire. Si usted apuesta 1 dólar, la probabilidad de ganar es 50%, mientras que la probabilidad de perder 1 dólar también es del 50%. Su ganancia o pérdida esperada es cero. Por la misma razón, llegan a la conclusión de que las ganancias y pérdidas operando futuros tienden a compensarse entre sí a largo plazo.
Pues bien, hay una falacia oculta en ese razonamiento. Abrir posiciones en futuros no es análogo a lanzar una moneda. Más bien, la analogía correcta sería la de una serie repetida de lanzamientos de moneda con un punto final estocástico. ¿Por qué? Porque el capital del que disponemos es limitado. Supongamos que estamos lanzando una moneda con un amigo y apostamos 1 dólar al resultado de cada lanzamiento. En algún momento, ya sea usted o su amigo, tendrá una racha de mala suerte y perderá varios dólares seguidos. Si un jugador se ha quedado sin dinero, el juego llegará a su fin. Lo mismo aplica al mercado de futuros. Si tenemos una serie de pérdidas en futuros, al final tendremos un margin call y tendremos que cerrar posiciones. Quedamos obligatoriamente fuera del juego, y por lo tanto no podemos recuperar lo que hemos perdido. De manera similar, en 1974 Franklin National Bank y Bankhaus I. D. Herstatt tuvieron una serie de pérdidas en sus posiciones en divisas y se fueron a la quiebra antes de poder recuperarse. Este fenómeno se conoce en teoría de la probabilidad como el problema de la ruina del jugador.
Lo que es una apuesta «justa» cuando lanzamos una vez una moneda, se convierte en un juego completamente diferente cuando consideramos una serie de lanzamientos de la moneda con un punto estocástico final. Las probabilidades del juego dependerán en este último caso de las cantidades relativas de capital en manos de los distintos jugadores.
Supongamos que consideramos un proceso de apuestas en el que ganamos 1 dólar con probabilidad p y perdemos 1 dólar con probabilidad q = 1 – p. Se empieza con una cantidad de dinero W. Si su dinero cae hasta cero, el juego se detiene. Su compañero de apuestas, la persona en el otro lado de su apuesta gana cuando Vd. pierde y pierde cuando Vd. gana, tiene una cantidad de dinero R. ¿Cuál es la probabilidad de que finalmente pierda todo capital W, dados p y R? A partir de la Teoría de la Probabilidad, la respuesta es:
(q/p)W + R – (q/p)W
Probabilidad de Ruina = ————————–, para p distinto de q
(q/p)W + R – 1
Probabilidad de Ruina = 1 – [W / (W + R)], para p = q = 0.5
Veamos un ejemplo: supongamos que Vd. tiene 10 dólares y su amigo tiene 100. Se tira una moneda al aire. Si sale cruz, su amigo le paga 1 dólar. Si sale cruz, le pagamos 1 dólar. El juego termina cuando el jugador se queda sin dinero. ¿Cuál es la probabilidad de que su amigo se haga con todo su dinero? A partir de la segunda ecuación anterior, tenemos p = q = 0.5, W = 10 y R = 100. Por lo tanto la probabilidad de perder todo el capital es:
1 – (10 / (10 + 100)) = 0.909
Es decir, Vd. perderá todo su dinero con un 91% de probabilidad en este juego supuestamente «justo».
Ahora ya sabe cómo ganan dinero los casinos. Su cuenta bancaria es más grande que la suya. Con el tiempo Vd. tendrá una mala racha, y tendrá que dejar de jugar (ya que los casinos no le prestarán capital infinitamente).
La probabilidad de ruina del jugador es un concepto realmente importante. Es cierto que las probabilidades están en contra del jugador en cada juego del casino: de forma especial en el juego del Keno, moderadamente contra el jugador de tragaperras, marginalmente contra el jugador de blackjack y dados (normas como «sólo se puede doblar en 10s y 11s» en el blackjack pretenden poner las probabilidades en contra del jugador, al igual que el uso de múltiples juegos de cartas, etc.). Sin embargo, la principal fuente de ganancias del casino es que la gente tiene dejar de jugar una vez que ha tenido una mala racha suficientemente grande, lo cual es inevitable (un montón de bebidas gratis servidas a los jugadores ayudan en este proceso. Desde el punto de vista del casino, la inversión en bebidas gratuitas funciona estupendamente).
Obsérvese que el capital (W o R en la ecuación) se define como el número de unidades de apuestas: 1 dólar en el ejemplo. Cuantas más unidades de apuestas se tengan, menor será la probabilidad de verse afectado por el problema de la ruina del jugador. Por lo que si usted se sienta en la mesa de blackjack con una apuesta mínima de 1000 dólares, tendrá que tener 100 veces el capital total de apuestas de alguien que se encuentra a las mesas con apuesta mínima de 10 dólares, con el fin de tener las mismas probabilidades contra la banca.
Una persona que tiene 1000 dólares de capital y apuesta 10 cada vez, tiene un total de W = 1000/10 = 100 unidades de apuesta. Esta es una relación bastante buena.
Sin embargo, una persona que tiene 10.000 dólares de capital y apuesta 1.000 dólares cada vez tiene W = 10000/1000 = 10 unidades de apuesta. Eso son unas probabilidades pésimas, da igual en qué juego. Son probabilidades de perdedor.
Gauss vs. Cauchy
Midamos la probabilidad con nuestra jarra de de mermelada. Podemos distribuir la mermelada como deseemos. Si ponemos todo en el punto x = 5, entonces diremos que «x = 5 se dará con certeza» o «x = 5 con probabilidad 1.»
A veces, la forma en que se distribuye la mermelada está determinada por una función simple. La distribución Normal o gaussiana distribuye la mermelada (probabilidad) a través de la línea real (de menos infinito a más infinito) usando la función de densidad:
f(x) = [1/(2p)0.5] exp (-x2/2), – ∞ < x < +∞
Con f(x) creamos la bonita curva en forma de campana que ya conocemos (x está en la línea horizontal, y f(x) es la curva azul por encima de él):
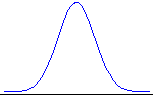
La mermelada (probabilidad) se unta entre la línea horizontal y la curva, por lo que la altura de la curva en cada punto (dada por f(x)) indica la probabilidad del punto relativa a otro punto. La curva f(x) se llama densidad de probabilidad.
Así podemos calcular la densidad de probabilidad para cada valor de x mediante la función f(x). Aquí tenemos algunos valores:
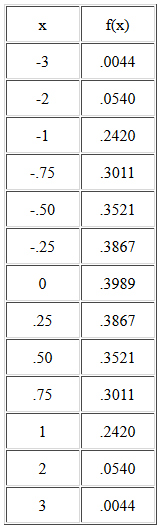
En el valor central x = 0, la densidad de probabilidad es más alta, y tiene un valor f(x)=0.3989. Alrededor de 0, la densidad de probabilidad se extiende simétricamente a cada lado.
El tarro entero de mermelada se unta por debajo de la curva entre –∞ y +∞. Así que la probabilidad total, el área total bajo la curva, es 1. En Cálculo Infinitesimal, el área bajo la curva se escribe como una integral, y puesto que la probabilidad total es uno, la integral de –∞ a +∞ de la función f(x) que esparce mermelada es 1.
La probabilidad de que x se encuentre entre a y b, a <x <b, es sólo el área bajo la curva (la cantidad de mermelada) medida desde a a b, como se indica en la porción roja del siguiente gráfico, donde a = – 1 y b = 1:
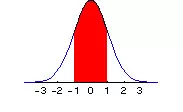
Si denotamos por simplicidad la integral de A a B de f(x) como:
I(a, b) f(x) dx.
Tenemos que I(a, b) f(x) dx es el área bajo la curva f(x) entre a y b. Y dado que la probabilidad total (área total bajo la curva) a través de todos los valores de x (de –∞ a +∞) es 1, tenemos que:
I(-∞, +∞) f(x) dx = 1
Introduzcamos un poco más notación: queremos expresar de forma abreviada la probabilidad de que x <b. Sin embargo, la probabilidad de que x <b es lo mismo que la probabilidad entre –∞ y b. Podemos escribir esto como F(b) tal que:
F (b) = I (-∞, b) f(x) dx = Área bajo la curva de menos infinito a b
Si por ejemplo b=0, tendríamos que F(b) gráficamente sería:
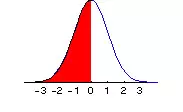
Ojo, es importante observar que el área bajo la curva en un punto es igual a cero, por lo que da igual si incluimos o no el punto x, ya que no cambia el valor de F(x). No obstante, para simplificar las explicaciones, diremos que el punto x sí está incluido en el cálculo de F(x).
F (x) toma valores entre 0 y 1, que corresponde a nuestra jarra de mermelada. Por tanto, F (-∞)=0, mientras que F (+∞) = 1.
La probabilidad de entre a y b, a <x <b, puede escribirse simplemente como F(b) – F(a). Y la probabilidad x> b se puede escribir como 1 – F(b).
Bien, veamos otra función diferente para esparcir la probabilidad, denominada densidad de Cauchy, cuya expresión es la siguiente:
g (x) = 1 / [p(1+x2)], – ∞ <x < +∞
Aquí tenemos una imagen mostrando la curva resultante:
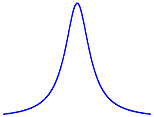
Como podemos ver es simétrica como la distribución Normal, pero está relativamente más concentrada alrededor del centro, y presenta unas colas más altas. Podéis ver una comparativa de ambas distribuciones en el siguiente gráfico:
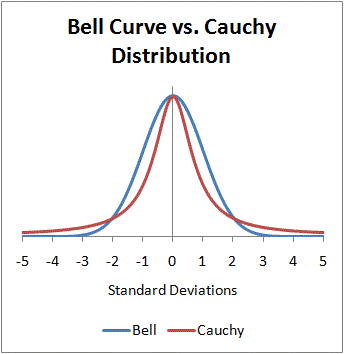
Veamos la siguiente tabla de valores de g(x):
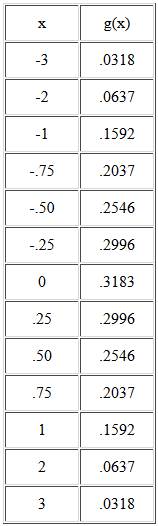
En ella podemos ver que, para cada valor de x, la densidad de Cauchy es menor que la densidad normal, al menos hasta que vayamos a valores extremos, tales como +/-2 o +/-3. Por ejemplo, en -3 la densidad de probabilidad de la distribución de Cauchy es g (-3) = 0.0318, mientras que para la distribución Normal, el valor es f (-3) = 0.0044. ¡Hay más de 7 veces más probabilidad de este valor extremo en la distribución de Cauchy que en la distribución Normal! En relación con a la Normal, la distribución de Cauchy presenta colas gruesas.
Como veremos más adelante, existen otras distribuciones que tienen más probabilidad en las colas que la Normal, y también más probabilidad en torno a 0). Pero ya que la probabilidad total debe sumar 1, habrá lógicamente menos probabilidad en los rangos intermedios. Tales distribuciones se llaman leptocúrticas. Las distribuciones leptocúrticas tienen más probabilidad en las colas y en el centro que la distribución Normal, y se pueden encontrar en todos los mercados: divisas, acciones, tipos de interés, materias primas… Aquellos que pretenden que las distribuciones empíricas de las variaciones de los precios en estos mercados son Normales en lugar de leptocúrticas están engañándose a sí mismos por desgracia.
Localización y Escala
Hasta el momento hemos visto que las densidades Normal y de Cauchy están centradas en cero. Sin embargo, ya que se define la densidad de todos los valores de x, –∞ <x <+∞, el centro puede estar en cualquier otra parte. Para mover el centro de cero a una ubicación m, escribimos la densidad Normal como:
f (x) = [1/(2p)0.5] exp(-(x-m)2/2), –∞ <x <+∞
Aquí tenemos una imagen de la distribución Normal después de desplazarla de m = 0 (en azul) a m = 2 (en rojo):
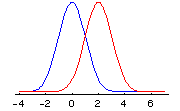
Para la densidad de Cauchy, la alteración correspondiente para incluir un parámetro de localización m es:
g (x) = 1 / [p (1 + (x-m)2)], –∞ <x <+∞
En cada caso, la distribución se centra ahora en m en lugar de cero. Obsérverse que hablamos del parámetro de ubicación m y no de la media m. La razón es simple: para la distribución de Cauchy, no existe una media sino un parámetro de localización, que muestra donde está centrada la distribución de probabilidad.
Para la distribución Normal, el parámetro de localización m es el mismo que la media de la distribución. Así, una gran cantidad de personas que sólo estén familiarizadas con la distribución Normal confunden los dos, aunque no son lo mismo.
Del mismo modo, para la distribución de Cauchy no existe la desviación típica ni la varianza (de hecho se considera que son infinitos). Pero hay un parámetro de escala c que muestra hasta qué punto se tiene que mover en cada dirección desde el parámetro de localización m, a fin de que el área bajo la curva se corresponda con una determinada probabilidad. Para la distribución Normal, el parámetro de escala c se corresponde con la desviación típica.
Veamos la densidad Normal escrita con la adición de un parámetro de escala c:
f (x) = [1 / (c(2p)0.5)] exp (-((x-m)/c)2/2), –∞ <x <+∞
A continuación se muestra un gráfico de la distribución Normal para diferentes valores de c:
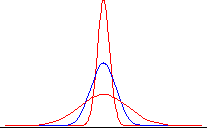
La curva azul representa c = 1, mientras que la curva de color rojo más apuntada se obtiene con c <1, y la curva roja aplanada se obtiene para c> 1.
Para la densidad de Cauchy, la adición de un parámetro de escala nos da el siguiente resultado:
g (x) = 1 / [cp (1 + ((x-m)/c)2)], –∞ <x <+∞
Al igual que hicimos con la distribución Normal, se divide (x-m) por c, y también multiplicamos toda la densidad por el recíproco de c. Gráficamente podemos ver en la siguiente figura cómo varía el aspecto de esta distribución en base a diferentes valores de c y m:
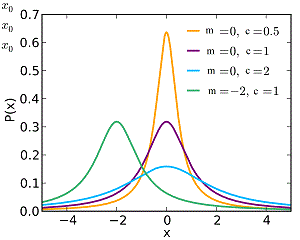
Como podemos ver, las operaciones con la localización y la escala están bien definidas, aunque no existan la media o la varianza.
La mayoría de las distribuciones de probabilidad que nos interesan en Finanzas se encuentran en algún lugar entre la Normal y Cauchy. Estas dos distribuciones forman los «límites», por así decirlo, de nuestra principal área de interés. Al igual que la alfombra de Sierpinski tiene una dimensión de Hausdorff que es una fracción mayor que su dimensión topológica de 1, pero menor que su dimensión euclidiana de 2, también lo hacen las distribuciones de probabilidad en la que estamos interesados principalmente: tienen una dimensión mayor que la dimensión de Cauchy de 1, pero menor que la dimensión Normal de 2. Ah pero, ¿las distribuciones también tienen dimensiones? Lo veremos en la siguiente entrega ;).
(Continuará…)
Saludos,
X-Trader