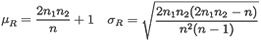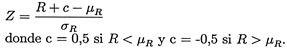X-Trader escribió: 13 Sep 2019 20:38
Si multiplicas por N el numerador y el denominador obtienes la expresión de Ralph Vince. Ahora ya solo falta averiguar por qué Ralph Vince pone c = -0.5.
Gracias, X-Trader.
Tal vez, en los sistemas de trading ganadores, haya un ligerísimo sesgo de dependencia positiva y raramente R supere a su Esperanza Matemática, 2WL/N+1,y, por ello, está fijo, en la fórmula que utiliza Ralph, el c=-0,5 (o sea, con signo negativo).
Tal vez porque difícilmente un sistema de trading ganador podría tener una ley de dependencia negativa.
Otra cosa es que en un sistema de trading neutro (ni claramente ganador, ni claramente perdedor), hallemos una ley de dependencia y entonces creemos un algoritmo que aprovechando la ley de dependencia el sistema de trading lo convirtamos en ganador. Pero entonces ese nuevo sistema tendría un número de rachas inferior a su esperanza matemática.
No sé si me explico.
¿Puede ser?
De todas maneras, aunque esta explicación podría, tal vez, justificar que Ralph tome signo negativo fijo en el corrector, continua siendo un misterio para mí porque tiene que haber un corrector, y más si tenemos en cuenta que algunas textos no incluyen el corrector +-0,5 en la fórmula de Z.
Saludos.