En multitud de ocasiones hemos podido escuchar a distinto tipo de gente la importancia del cierre de una sesión como dato más característico de la misma, es más, personajes tan célebres como Charles Henry Dow, lo llegó a enunciar en uno de sus principios tan conocidos por todos, en donde se nos invita a usar los cierres en nuestros «charts», despreciando los típicos gráficos en donde empleamos máximos y mínimos.
Hoy día la mayor parte de los analistas usa gráficos de barras o de velas y pocos son los que usan cierres en sus análisis, ya que debemos aprovechar al máximo toda la información de los precios que nos brinda el mercado. Pero todo lo contrario ocurre con muchos indicadores, donde con frecuencia los programas que usamos para analizar los gráficos, los incorporan por defecto, vamos, que resulta todo una paradoja.
Una vez detectadas dichas diferencias, y con ánimo de comprobar si es más ventajoso el uso del cierre en comparación con otros datos como es: máximo + mínimo / 2, o máximo + mínimo + cierre / 3, vamos a tomar una media móvil simple, calculada con cada una de ellos. La idea es demostrar, si usando datos que incorporen más información de la sesión, obtenemos mejores resultados.
Por lo tanto para abordar el estudio, pasaremos cada una de las tres medias anteriores, como sistema de «trading», por 5 valores durante el periodo (96 – 02), periodo suficiente donde encontramos ciclos alcistas y bajistas. Pero para que la comparación sea completa, voy a llevar a cabo una optimización entre las 100 primeras medias, para así comparar las curvas de beneficio de cada una de ellas.
En primer lugar y dado que hemos hablado de la optimización, debo añadir que soy partidario de su utilización, ya que para predecir el comportamiento de una acción, los analistas técnicos consultamos el pasado, es decir hacemos eco de la frase que dice: «El presente es función del pasado y el futuro es función del presente». Por lo tanto una media que se comporte bien hoy y ayer, tiene muchas probabilidades de hacerlo bien mañana y digo bien que no es lo mismo que muy bien.
Pero también es verdad que para hacer un uso correcto de la optimización debemos de realizar otro tipo de análisis denominado análisis de robustez.
Este tipo de prueba lo que busca es la estabilidad de sistema el día de mañana. Es la cualidad que te permite esperar en el futuro unos resultados similares a los del pasado. Es decir lo que buscamos con este análisis es identificar una zona donde la variación de los óptimos no nos lleve a variaciones fuertes del beneficio. De forma que un sistema inestable en un cambio secundario de mercado puede producir resultados distintos a los del pasado.
De esta forma enfrentamos la robustez contra el máximo beneficio. Ya que en una optimización lo primero que muchas veces buscamos es el beneficio máximo, pero como ya hemos explicado, puede que este beneficio sea puntual, es decir obtenido por un solo optimo, distando del resto de beneficios, existiendo un «curve fitting» o ajuste la curva de precios por razones naturales.
Debo añadir que dicho análisis y para alivio de muchos es visual, no es matemático ni estadístico, por lo que resulta muy sencilla su interpretación. Para ello lo primero que se debe hacer es graficar los óptimos y el beneficio conjuntamente. En nuestro caso al tener un solo óptimo resulta de gran sencillez, pero también podemos graficar 2 óptimos, utilizando gráficos en 3-D como los que podemos ver abajo.

Estos tres casos son las situaciones clásicas que nos encontramos en los análisis de superficie o de robustez:
-Figura 1 (Bueno): Existe un pico dominante sobre el resto, sin ser apuntado como en los otros ejemplos, lo que nos lleva a confirmar la validez del óptimo obtenido con mayor beneficio
-Figura 2 (Malo): Encontramos continuos y similares máximos, con cierto grado de apuntamiento cada uno de ellos. Podemos ver como una variación pequeña en un óptimo puede llevarte a una caída fuerte de los beneficios.
-Figura 3 (Bueno – Revisar): No hay un máximo dominante sobre el resto, pero si una zona un tanto robusta, con un pico no muy pronunciado. En principio a priori se puede considerar como bueno, pero sólo en la zona donde se produce dicha situación, acotando la escala con mucho cuidado.
Una vez realizada la conveniente clasificación, estamos ya en condiciones de comenzar a realizar el pertinente estudio.
La forma de desarrollarlo va a ser igual en las cinco acciones (BBVA, BSCH, ELE, TEF y ALT), por un lado visualizaremos las curvas de beneficios correspondientes a el cierre, máximo + mínimo/2, máximo+mínimo+cierre/3, ordenando éste de mayor a menor y comparando la forma de cada una. Posteriormente realizaremos una representación gráfica de cada optimo ordenado de mayor a menor, con su respectivo beneficio, para comprobar las zonas donde existe robustez.
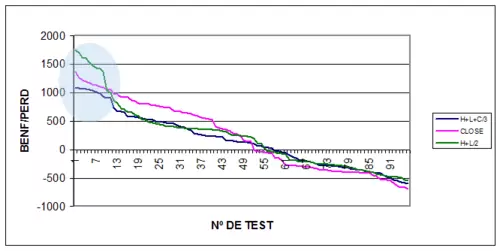
El máximo beneficio se obtiene con otra curva distinta al cierre, como es el máx+min/2 y además en este caso la zona señalada como máximo beneficio presenta mayor robustez que el resto de curvas, según la clasificación que hemos comentado. Este es el clásico ejemplo modelo que deberíamos obtener siempre, donde el máximo beneficio coincide con la zona robusta.
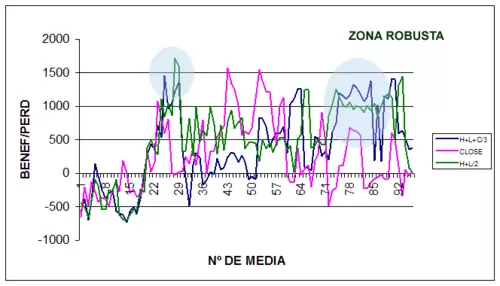
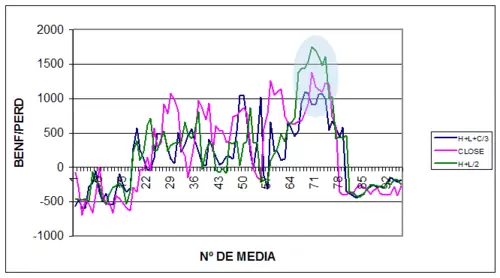
Respecto al tema de la robustez, podemos apreciar que el optimo con mayor beneficio de la curva max+min/2 no es sólido y por tanto no lo debemos considerar como apropiado. Pero en dicha curva existe una zona con menores beneficios que el anterior optimo, pero mas contundentes ante variaciones del mismo, es la zona señalada en el gráfico.
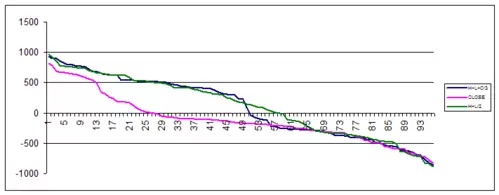
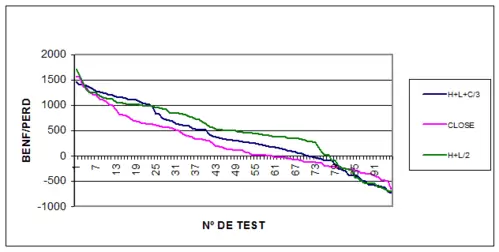
Como en casos anteriores la curva de beneficios dominante es la de max+min/2. Pero el óptimo con el que se obtiene mayores beneficios no es robusto. Por lo tanto debemos recurrir al análisis visual para ver que zona es más sólida. En este caso, encontramos una zona más o menos robusta en las curvas de óptimos que usan max+min/2 y cierre, sobre todo esta última, en la parte final de la misma.
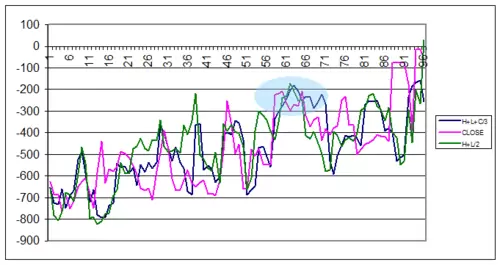
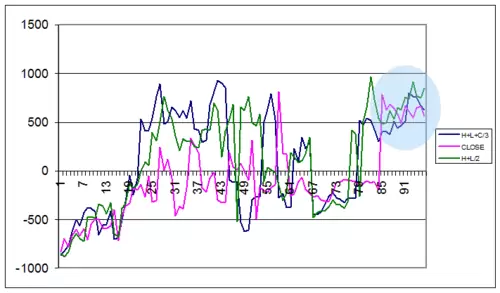
Este es el típico ejemplo donde se nos muestra cómo no siempre una estrategia es beneficiosa en todos los valores, es más, apenas se sitúa en terreno positivo.
A pesar de ello, y como ya va siendo costumbre en los demás casos, vamos a seleccionar un área que cumpla los requisitos de rigidez. Dicha zona la hemos subrayado dentro de un circulo en el grafico y corresponde a la curva max+min+cierr/3.
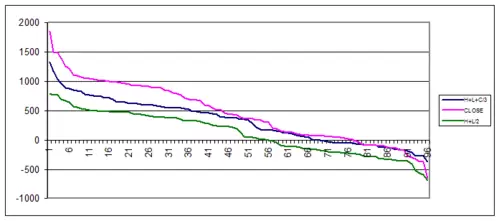
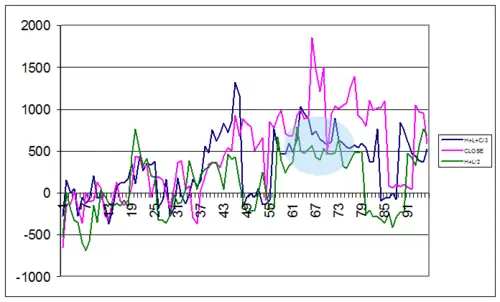
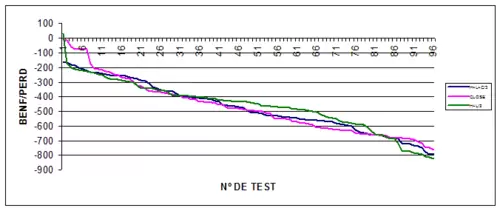
En este caso no es el max+min/2 el dato mas beneficioso si no el cierre, como vemos en el primer gráfico, pero el análisis visual nos muestra las deficiencias de seleccionar el cierre como dato de cálculo para nuestra media, ya que obtenemos mayor beneficio pero menor robustez. Si tendríamos que elegir una zona, a pesar de que no existe una área dominante de máximos y de cierta continuidad, escogeríamos la zona señalada en el dibujo correspondiente al max+min/2.
Conclusiones
Con este estudio hemos intentado aclarar la grave problemática a la que nos enfrentamos cuando utilizamos una media móvil a la hora de escoger el periodo y el dato para su cálculo. Todo esto tiene su lógica desde la perspectiva de aceptación del concepto de optimización, que a priori después de analizar las zonas de robustez puede ser considerado como bueno. Pero debo añadir que para aceptar la validez de dichos análisis, cuanto mayor sea el número de tests para analizar, mejor. Situación que se produce a medida que introducimos más óptimos, pero sin abusar de ello porque caeríamos en la denominada sobreoptimización del sistema, característica que nos lleva a escoger óptimos impropios. Una vez seleccionado el óptimo adecuado, se utilizan las técnicas de «Walk Forward» o «Out of Sample» para terminar de declarar a un sistema como adecuado para ser utilizado. Dichas técnicas serán tratadas en estudios posteriores, de momento sólo hacemos caso de la robustez.
Para terminar sólo quiero decir después de lo que he presentado, que no siempre o mejor dicho casi nunca el optimo con mayor beneficio es el más robusto, además la curva que obtiene mayor beneficio y mayor robustez es la curva de max+min/2. Por lo tanto sería el dato adecuado que deberíamos utilizar en el cálculo de nuestras medias e incluso me atrevería a decir que deberíamos usarlo en los osciladores también, cuando los incorporamos a nuestros sistemas de «trading».
Roberto Pérez aka NoiseTrader ([email protected])
*Desde aquí, deseo dar las gracias a Iván Domenech por su colaboración