No es la primera vez que tratamos en esta web el uso de indicadores para determinar el régimen en que se encuentra el mercado (esto es, si está en tendencia o no). Sirvan como ejemplo el ratio basado en el número pi que vimos en el artículo El Poder de Pi o el debate que actualmente mantenemos en el Foro sobre el Exponente de Hurst.
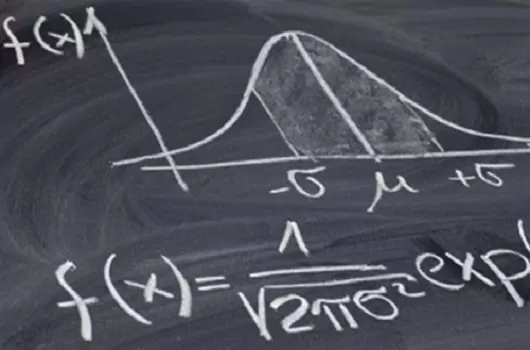
En el caso del indicador que nos ocupa, el Market Meanness Index (abreviado MMI), el cual podríamos traducir como índice de “medianez” del mercado, también nos permite clasificar el estado del mercado, indicándonos si el precio está en tendencia o no utilizando un algoritmo puramente estadístico, no basado en volatilidad, tendencias o ciclos sino en contar desviaciones con respecto a la mediana de la distribución de precios. Con ello se pretende determinar la “medianez” del precio, esto es, su tendencia a revertir a la mediana tras haber iniciado un movimiento en una dirección.
Para ello, deberemos aplicar la regla de los tres cuartos: la idea básica aquí es que una serie cualquiera de números aleatorios revertirá a la mediana con una probabilidad del 75%. O dicho de otro modo, si nos fijamos en una secuencia aleatoria de precios y el cierre de ayer está por encima de la mediana, en el 75% de los casos el precio de hoy será más bajo que el de ayer; de forma análoga, si el precio de cierre de ayer está por debajo de la mediana, existe un 75% de posibilidades de que el precio de hoy sea más alto.
La demostración de esto es relativamente sencilla: supongamos una serie de precios con mediana M. Por definición de lo que es una mediana, la mitad de los precios serán menores que M y la otra mitad mayores (al fin y al cabo la mediana es la medida de posición central que divide exactamente en dos una distribución). Combinemos ahora los precios de la serie en pares de la forma (Py, Pt), donde Pt es el precio consecutivo en la serie a Py. Por tanto, cada par representa una variación de precios de Py a Pt. A partir de esos pares podemos construir los siguientes cuatro grupos:
1. (Pt<M, Py<M)
2. (Pt<M, Py>M)
3. (Pt>M, Py<M)
4. (Pt>M, Py>M)
Estos cuatro grupos tienen, obviamente, el mismo número de elementos – es decir, un cuarto de todos los cambios de precios al pasar de Py a Pt, suponiendo que Py y Pt no están correlacionados (aquí quizás podríamos poner alguna objeción, más sobre esto en un momento). Dicho esto, ¿cuántos pares de precios revertirán a la mediana? Serán todos los pares que cumplan esta condición: (Py<M y Pt>Py) o (Py>M y Pt<Py).
La primera condición se verifica en la mitad de los precios del grupo 1 (en la otra mitad se cumple que Pt<Py) y en todo el grupo 3 (Pt siempre es mayor que Py). Así que la primera condición es cierta para 1/2 x 1/4 + 1/4 = 3/8 de todos los cambios de precios. Del mismo modo, la segunda condición es cierta en la mitad de los precios del grupo 4, y en todo el grupo 2, por tanto, también para 3/8 de todos los cambios de precios. Sumando tenemos 3/8 + 3/8 = 6/8, es decir, 75%. Esta es la regla de tres cuartos de las diferencias de números aleatorios.
¿Cómo aplicamos esto en la práctica en el trading? Muy sencillo: sabemos que una distribución perfectamente aleatoria tendrá un MMI del 75%, mientras que valores bajos del MMI será un signo claro de tendencia. Dicho de otro modo, un MMI descendente desde el 75% será señal de una tendencia está iniciándose mientras que un MMI ascendente hacia la zona de 75% será indicativo de un posible mercado lateral. Esto podemos verlo claramente en el siguiente gráfico diario del Crude Oil donde hemos representado la línea del 75%:
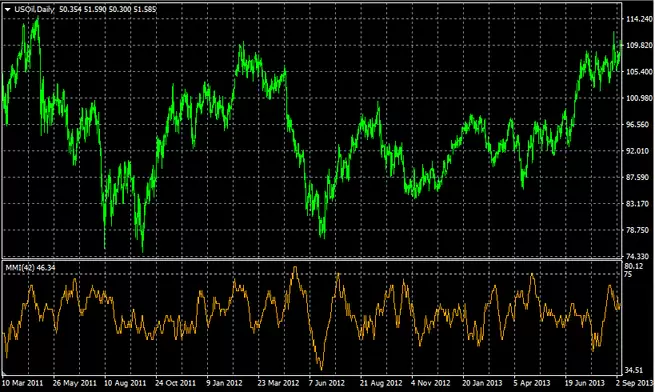
Por cierto, si quieren jugar con el indicador en Metatrader 4 pueden descargarlo en este hilo del Foro.
Decíamos hace un momento que uno de los requisitos para que la regla de los tres cuartos se verifique es que los elementos de la serie analizada deben ser estadísticamente independientes (i.e. no existe correlación entre ellos). Si bien el MMI puede aplicarse al precio asumiendo este supuesto (algo no muy realista), lo ideal sería aplicarlo a las variaciones de los precios.
Asimismo conviene tener en cuenta que por el hecho de que el MMI llegue al 75% no significa necesariamente que el precio vaya a revertir a la mediana. Ello será así para los precios contenidos en la muestra analizada pero no para el último precio.
Seguramente el lector esté pensando ahora mismo para que nos sirve el MMI realmente. Aunque no parezca evidente, es un excelente filtro para sistemas seguidores de tendencia, incrementando su probabilidad de éxito. Confieso que aún no lo he probado personalmente pero he visto algunos estudios en los que filtrar sistemas tendenciales con el MMI mejora notablemente el Profit Factor de este tipo de estrategias… aunque eso me lo dejo para un próximo artículo ;).
Saludos,
X-Trader