Terminamos la serie sobre Mel Widner analizando otro de sus indicadores: los Soportes y Resistencias Automatizados y su versión en formato oscilador. Estos indicadores vieron la luz en el número de mayo de 1998 de la revista Stock and Commodities y con ellos podemos calcular matemáticamente niveles de soporte y resistencia. Así, Widner define en ese artículo soporte y resistencia de la siguiente manera:
Para un período de N barras, siendo N impar e igual o mayor que 3), definimos la barra central de ese período como M = (N-1)/2. Entonces diremos que:
- Tendremos un nuevo nivel de soporte si se verifica que el mínimo en la barra central M es el menor mínimo en el período N. El nivel de soporte pasará a ser precisamente ese mínimo.
- Se formará un nuevo nivel de resistencia si se verifica que el máximo en la barra central M es el mayor máximo en el período N. El nivel de resistencia pasará a ser precisamente ese máximo.
Por ejemplo, si tomamos un período de 9 barras, diremos que la barra central es la cuarta. Si en esa cuarta barra se forma el mayor máximo o el menor mínimo del período de 9 barras, diremos que en ese nivel existe una resistencia (mayor máximo) o un soporte (menor mínimo).
Para que quede más claro, aquí tenéis una explicación gráfica del asunto:
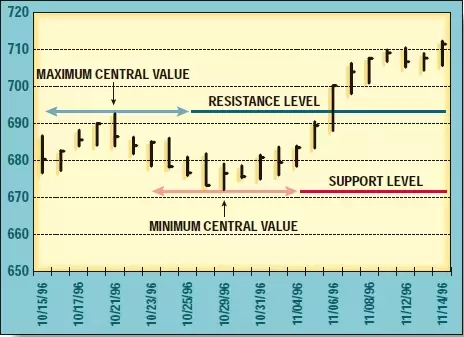
Si os fijáis, realmente el concepto no es muy diferente de la idea de Fractal definida por Bill Williams y que vimos en este artículo.
Como hemos visto en anteriores artículos, a Mel Widner le gusta convertir todas sus ideas en osciladores y en este caso no iba a ser menos. A raíz del problema que supone tener múltiples niveles de soporte y resistencia representados en el gráfico a medida que pasa el tiempo, Widner decidió desarrollar una fórmula que tuviera en cuenta los últimos 6 soportes y 6 resistencias, de tal forma que cada vez apareciera un nuevo nivel de soporte o resistencia, se eliminase de la fórmula el nivel más antiguo.
A partir de los últimos 6 niveles de soporte y resistencia, Mel Widner crea dos osciladores denominados WSO (Widner Support Oscillator) y WRO (Widner Resistance Oscillator), cuyas fórmulas son las siguientes:
WSO = 100*(1 – (INT (S1/C) + INT (S2/C) + INT (S3/C) + INT (S4/C) + INT (S5/C) + INT (S6/C)) / 6)
WRO = 100*(1 – (INT (R1/C) + INT (R2/C) + INT (R3/C) + INT (R4/C) + INT (R5/C) + INT (R6/C)) / 6)
Donde:
C es el cierre de la barra actual
S1, S2, S3, S4, S5, S6 son los seis últimos niveles de soporte.
R1, R2, R3, R4, R5, R6 son los seis últimos niveles de resistencia.
INT es la función entero, que toma la parte entera de una división, eliminando los decimales.
El aspecto visual de estos osciladores es el siguiente, siendo el WSO la línea en rojo y el WRO la línea en azul:
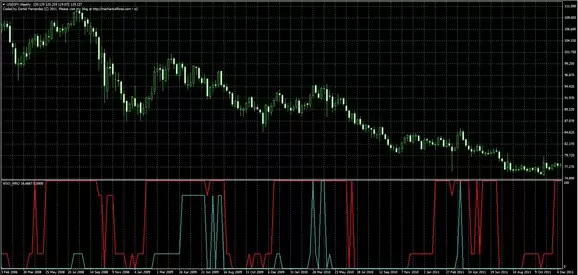
Como podemos ver, ambos osciladores se mueven entre los valores 0 y 100. Cuando uno de los indicadores alcanza el nivel de 0, significa que el precio está por debajo de todos los niveles, mientras un valor de 100 indica que estamos por encima de todos los niveles. En particular, podemos considerar las siguientes reglas:
- Un WSO ascendente indica que se está formando un soporte. Cuando WSO=100 la fortaleza de los soportes será máxima.
- Un WRO ascendente también es signo de mercado alcista. Cuando WRO=100 se estará confirmando una rotura de resistencias.
- Un WRO descendente será indicativo de que se está formando una resistencia. Cuando WRO=0 estaremos ante una fuerte resistencia.
- Un WSO descendente es una señal de mercado bajista. Cuando WSO=0, se confirma una rotura de soportes a la baja.
Por ejemplo, si el oscilador WSO está en 100 y el WRO está en 50, significará que estamos por encima de todos los niveles de soporte pero solo por encima de la mitad de las resistencias. En esta situación podríamos interpretarla, por ejemplo, como que se está produciendo un retroceso dentro de un movimiento alcista.
Ahora es el turno de los lectores: en el Foro tenéis la versión de WSO/WRO para MetaTrader 4, que podéis descargar desde aquí.
Sobre este indicador se me ocurren algunas ideas interesantes para experimentar como insertar medias móviles (suavizaríamos aún más su comportamiento). De hecho una de las estrategias que Widner sugiere en su artículo, con muy buenos resultados en backtest, es la siguiente:
Compra si WSO > Media Móvil de WSO en las 4 barras previas o si Media Móvil de WSO es mayor de 95 durante 30 días. El cierre de las posiciones se realiza mediante trailing stop.
Otra idea interesante a explorar sería combinar los osciladores en diferentes timeframes para tener una composición en diferentes plazos de la posición del precio con respecto a los soportes y resistencias.
Sin lugar a dudas, de los tres indicadores que hemos visto en esta serie de artículos sobre Mel Widner, posiblemente este sea el que más juego da. Como siempre, espero sus comentarios y sugerencias en el Foro.
Saludos,
X-Trader
ARTÍCULOS RELACIONADOS
Mel Widner I
Mel Widner II