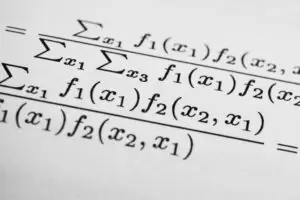En este artículo introducimos las Cadenas de Markov como la base de algunas estrategias utilizadas por la gestora Renaissance de Jim Simons, probablemente el único matemático que ha conseguido descifrar los mercados financieros. En el artículo se aplica una cadena de Markov muy simple de 4 estados para localizar patrones en los retornos de los precios que pueden ser explotados mediante una sencilla estrategia.
Es posible que haya oído hablar de Jim Simons, un matemático que trabajó descifrando códigos para la agencia nacional de seguridad americana durante la guerra de Vietnam aparte de contribuir a la teoría de cuerdas y a muchas otras áreas de la física.
Aunque Jim Simons es más conocido por su gestora Renaissance, creada en 1988 y que opera el Medallion Fund, un fondo que casi nunca pierde dinero. De hecho, el peor resultado en periodos de 5 años ha sido de un -0.5%. Invertir 1.000 dólares cuando comenzó el fondo ahora serían 13.8 millones de dólares. Impresionante…
Pues gran parte de la operativa de Jim Simons está basada en Cadenas de Markov, aunque evidentemente a un nivel matemático muy avanzado. Hoy solamente rascaremos un poco en la superficie de este tema.
De Qué Se Trata
Una cadena de Markov es un proceso estadístico que establece cierta dependencia entre un estado y el estado anterior. Es decir, solo tiene memoria del estado precedente y lo demás no cuenta. En finanzas esto es sencillo de entender. Supongamos que un estado significa retornos positivos. Y el otro estado, lógicamente, son retornos negativos. Así que una cadena de Markov podría decirnos cuál es la probabilidad de que hoy haya subidas si ayer hubo caídas. A continuación vamos a ver un ejemplo fuera de las finanzas que nos permitirá entenderlo:
El Mercadona de VillaArriba sabe que el 20% de la gente que compra fregasuelos un mes no vuelve a comprarlo al mes siguiente. Y también saben que el 30% de los que no han comprado fregasuelos este mes sí que lo comprará el mes siguiente. A este Mercadona acuden 1000 personas este mes, y de esos 100 compraron fregasuelos. ¿Cuántos lo comprarán el mes próximo? ¿Y dentro de dos meses?
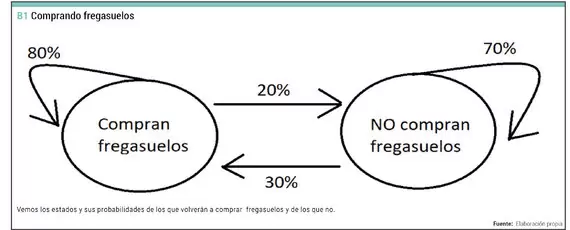
Dicho de otra forma: el 80% de los que compran fregasuelos este mes repiten su compra al mes siguiente, y el 70% de los que no compran fregasuelos este mes tampoco lo compran al mes siguiente. En realidad es un ejemplo bastante realista. En una pareja que viven juntos suele ser la misma persona la que compra este tipo de productos y la otra nunca o casi nunca se ocupa de ello.
Con la información aportada se puede construir la matriz de probabilidades:

Que si la multiplicamos por la matriz de personas que acuden al Mercadona pues nos tiene que dar el número de personas que el mes siguiente compra (C) o no compra (N):

Para multiplicar estas matrices hay que recordarse del álgebra, ya sabe, filas por columnas… Lo más sencillo es utilizar Excel. En Excel usamos la función MMULT(), seleccionamos la fila y luego la matriz de probabilidades. El primer elemento sale 350. Si marcamos los dos elementos, pulsamos F2 y luego Ctrl+Shift+Enter pues nos sale el vector fila completo: (350, 650).
La solución por tanto es que el primer mes comprarán fregasuelos 350 personas y 650 no lo compraran.
¿Y el siguiente mes? Para ello hay que tener en cuenta que, al igual que en probabilidades simples, la probabilidad de una segunda ocurrencia de algo es la probabilidad inicial multiplicada por sí misma, así que para el segundo mes tenemos que calcular la matriz producto:

Para esto se puede hacer el mismo procedimiento en Excel pero ahora marcaríamos 4 casillas para tener el resultado anterior de 2×2.
De la misma manera calculamos el número de personas para el segundo mes:

Es decir, el segundo mes 475 personas comprarán fregasuelos y 525 no lo comprarán.
Cómo Aplicamos Todo Esto a los Mercados
Pues como decía anteriormente podemos pensar en algo muy sencillo con dos estados. Cogemos los retornos del SP500 desde 2001; es decir, 20 años, y con la función JERARQUIA de Excel hacemos un ranking por retornos, de menor a mayor. Si dividimos el número de ranking entre el total de datos (5088) entonces tenemos el percentil que ocupa y así podemos calcular su estado de los dos posibles.
En este punto es posible que Vd. piense que me estoy complicando demasiado, ya que solo serían retornos positivos o negativos, así que sobraría el ranking. Pero suceden dos cosas:
- No tiene por qué haber simetría (el cero no tiene que dividir los resultados en dos partes iguales).
- El método del ranking nos va a servir para aumentar el número de estados posteriormente.
Ahora con una función CONTAR.SI ya podemos obtener la matriz de ocurrencias:
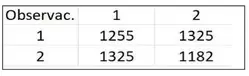
Si queremos las probabilidades solo hay que dividir entre el total de datos. Si el mercado fuera 100% aleatorio entonces esperaríamos 5088/4 = 1272 ocurrencias de cada estado.
Sin embargo vemos que es ligeramente más probable pasar del estado 1 al 2 (y viceversa) que de permanecer en el mismo estado.
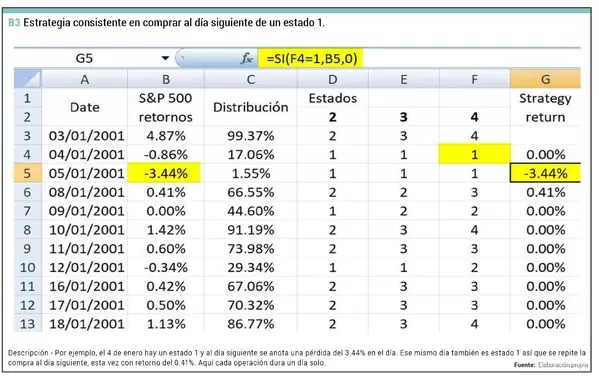
De hecho, sabemos que el mercado tiene una cierta tendencia a girarse al lado contrario del cierre anterior. En la imagen anterior vemos cómo el primer día de trading de 2001 se sube un 4.87% (estado 2) y al día siguiente se tiene un retorno negativo perteneciente al estado 1. Este día muy alcista está prácticamente en lo más alto de los percentiles, con un 99.37%.
Y luego tenemos el 5 de enero que se cae un 3.44%, es el percentil 1.55% y por tanto el estado 1. Al día siguiente hay un cambio al estado 2.
Tal y como comentaba esto no está necesariamente centrado en el cero así que mirando entre los datos veo que el percentil del 50% es un retorno del 0.08%. Retornos mayores son el estado 2; y retornos menores, aunque sean positivos, son el estado 1.
Añadiendo Estados
Ahora que hemos explicado el procedimiento ya se puede extender a más estados, y no hace falta ni siquiera saber cuáles son los umbrales entre un estado y el siguiente, ya que como acabo de explicar esto depende del total de los datos. El resultado para 4 estados es el siguiente:
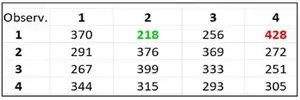
Lo que nos dice que es muy probable que después de un día muy bajista (estado 1) venga un día muy alcista (estado 4 con 428 ocurrencias). Y será raro que venga un día intermedio-bajista (estado 2 con solo 218 ocurrencias).
En Resumidas Cuentas
Así que para terminar me voy a construir un sistema de trading muy sencillo: si hoy es estado 1 entonces mañana compro el SP500; es decir, del cierre de hoy al cierre de mañana. Si ayer hubo estado 1 entonces hoy se anota la ganancia del día pues se asume que es lo que se gana al hacer la compra (no se incluyen comisiones y se asume que operamos justo por el nominal).
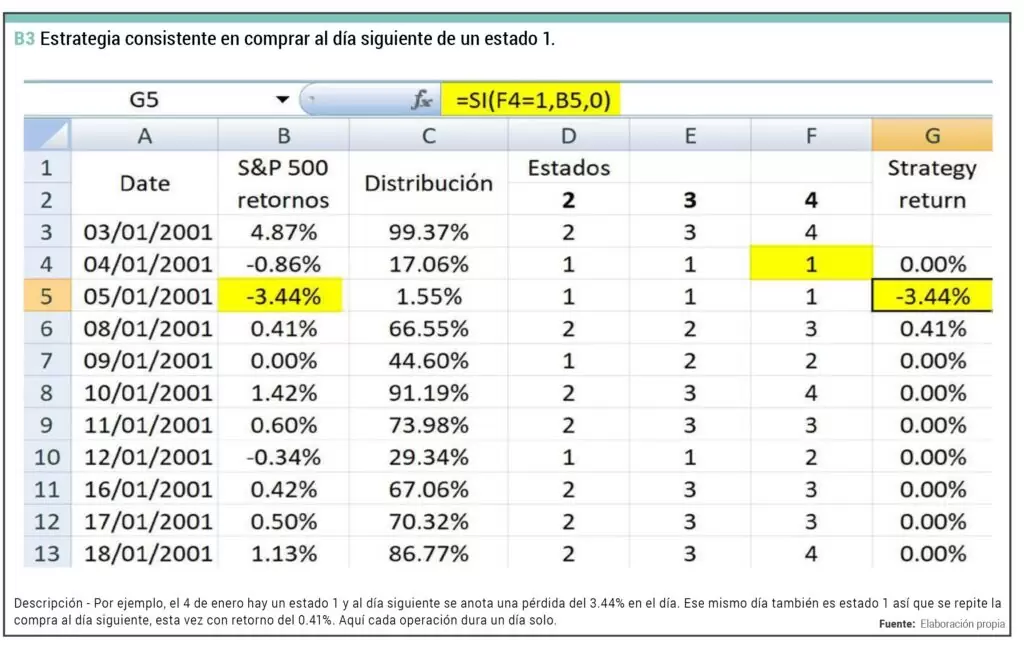
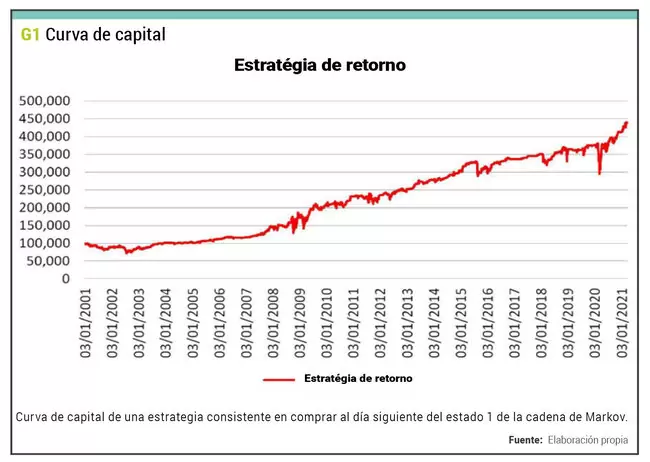
Y ahora ya puedo acumular los resultados de la columna que tiene la estrategia. La simulación comienza con capital inicial de 100.000 dólares, y resulta la siguiente curva de capital:
Sobre el Autor
Óscar G. Cagigas es Ingeniero de Telecomunicaciones por la Universidad de Cantabria. También fundador de Onda4.com, un portal que proporciona productos y servicios de consultoría financiera. Podéis contactar con él en onda4.com[a]gmail.com
Artículo publicado en el número de mayo de 2021 de la revista TRADERS’. Regístrate en www.traders-mag.es de manera completamente gratuita para acceder a más artículos como este.