Dedicado a Javier Rubio y Saúl Ávila por abrir el debate 😉
El pasado jueves asistí a la entrega de premios de la VIII Edición de Robotrader (por cierto, podéis ver el vídeo del evento aquí) y en el debate posterior que tuvimos mientras nos tomábamos unas copas con lo más granado del trading cuantitativo ibérico (allí estaban entre otros Rupertacho, Jesús Illescas, Raúl Gallardo, Tiotino, Javier Alfayate, Jorge Ufano o Roboco, así como algunos de los ganadores de la competición como AL-G, Carlos Grima o Miguel Ángel Jodra), Javier Rubio nos planteó la siguiente cuestión: ¿por qué el drawdown crece con el tiempo? ¿Por qué el drawdown es mayor para el backtest de un sistema probado en un histórico de 10 años que en uno de 5 años?
Aunque explicar aquello entre mojitos y gin-tonics sabíamos que iba a ser complicado, lo cierto es que Roboco hizo un apunte muy bueno: echad un vistazo al artículo de Magdon-Ismail, M. y Atiya, A.F. titulado Maximum Drawdown publicado en Risk Magazine en 2004.
Para remate, la misma cuestión me la vuelve a plantear unos días después del evento mi amigo Saúl Ávila así que… todo apuntaba en una sola dirección: ¡había que dedicar un artículo a esta cuestión en X-Trader.net!
Los Preliminares: ¿Qué es el Drawdown?
Supongo que si Vd. es lector habitual de X-Trader.net no tendrá dudas sobre lo que es el Drawdown y el Máximo Drawdown de una estrategia. No obstante, vamos a darle un rápido repaso. Siguiendo a Magdon-Ismail y Atiya, tenemos que el Drawdown para una curva de rendimientos acumulados X(t) de una estrategia es simplemente la diferencia entre el máximo de rendimiento obtenido y el rendimiento acumulado actual.
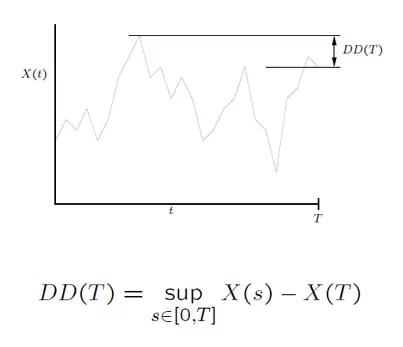
Por su parte, el Máximo Drawdown se define como la máxima pérdida producida entre un pico y un valle de la curva:
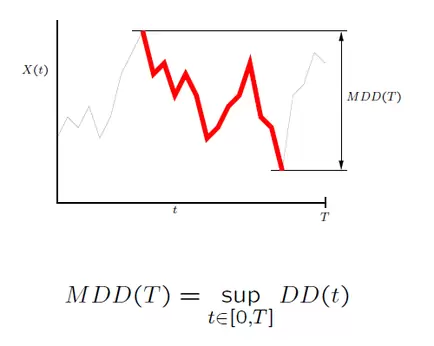
Ahora que ya tenemos las definiciones pertinentes, veamos cómo se relaciona todo esto con el tiempo.
La Relación entre el Máximo Drawdown Esperado y el Tiempo
Toca ahora ponerse un poco duro matemáticamente (aunque prometo que será solo un momento y que incluiré algunas explicaciones intuitivas para los que se pierdan con las fórmulas).
Bien, supongamos que el valor de una cartera sigue un movimiento browniano tal que:
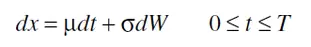
Donde t está medido en años, μ es el rendimiento medio por unidad de tiempo, σ es la desviación típica de los rendimientos por unidad de tiempo y dW es un incremento de Wiener.
Dicho de otro modo: lo que queremos representar es que el comportamiento de las variaciones del valor de una cartera es el de un paseo aleatorio.
Por otro lado, partimos del supuesto de que el Drawdown se comporta como un movimiento browniano reflejado tal que:
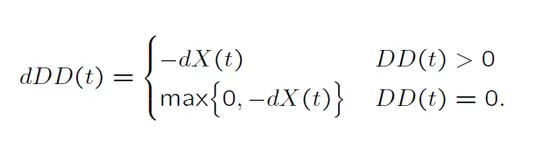
Intuitivamente podemos decir que el comportamiento del Drawdown se asemeja al movimiento de una partícula confinada en el semieje positivo. Cuando la partícula alcanza la frontera (0) es reflejada, alejándose de dicha frontera.
En base a estos supuestos, Magdon-Ismail y Atiya derivan la esperanza matemática del Máximo Drawdown obteniendo las siguientes expresiones cuando T tiende a infinito:
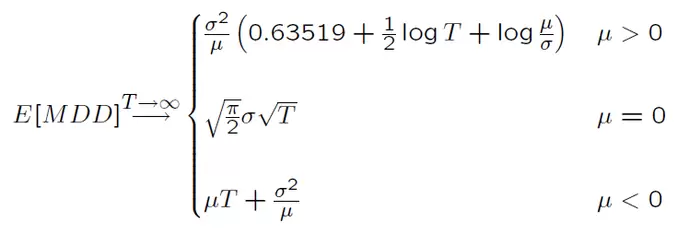
Seguramente nuestros lectores más quant entiendan las implicaciones de la expresión anterior, pero por si acaso se lo traduzco: la implicación más importante de este resultado es que el Máximo Drawdown aumenta con el tiempo y, además, lo hace de forma diferente en función de cómo sea la rentabilidad media esperada. En particular:
- Si la estrategia es ganadora (μ>0), el Máximo Drawdown aumenta lentamente, a razón de 0.5logT.
- En el caso de que la estrategia tenga una rentabilidad esperada nula (μ=0), el Máximo Drawdown aumenta algo más rápido, a razón de raíz de T.
- Finalmente, si la estrategia es perdedora (μ<0), el Máximo Drawdown aumentará más rápido, en base a T.
La evolución en el tiempo de la relación entre el Máximo Drawdown y la rentabilidad de una estrategia se ve claramente en el siguiente gráfico:
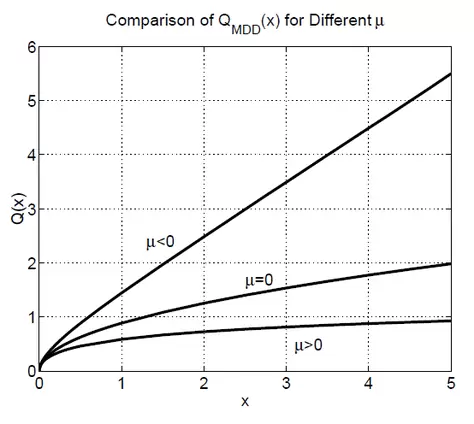
Implicaciones
El análisis que acabamos de ver de la relación entre el Máximo Drawdown y la rentabilidad esperada de una estrategia a lo largo del tiempo, nos invita a realizar algunas reflexiones de cierto calado:
- Como acabamos de ver, independientemente de la velocidad a la que lo haga, el Máximo Drawdown siempre crecerá a medida que pasa el tiempo. Ello tiene sentido ya que debemos considerar que, a medida que realizamos un mayor número de operaciones, más aumentará la probabilidad de tener una mala racha duradera, lo que en definitiva ampliará la cuantía del drawdown. Esto explicaría por qué generalmente el backtest de un sistema durante, por ejemplo, 10 años presenta un Máximo Drawdown peor que si lo hubiéramos realizado con 5 años de histórico.
- Si además reinvertimos los beneficios obtenidos en la operativa, tendremos como resultado que el Máximo Drawdown aumentará con el balance de nuestra cuenta, mientras que los beneficios de un sistema (incluso aunque sea ganador) solo crecerán de forma proporcional al tiempo (esto es, más despacio que el Máximo Drawdown).
- Combinando ambos efectos (esto es, cuanto más tiempo pase y más beneficios reinvirtamos), más amplificaremos nuestro Máximo Drawdown, lo que en la práctica se traducirá en que, en algún momento del tiempo, el Máximo Drawdown terminará por superar al valor de nuestra cuenta.
Todos estos resultados me llevan a plantearme algunos interrogantes que tienen mucha miga:
- ¿Hasta qué punto el Máximo Drawdown es una buena medida del riesgo de una estrategia?
- ¿Debemos considerar un horizonte de inversión antes de evaluar el riesgo máximo de la operativa?
- ¿Sería una buena estrategia de gestión monetaria no incrementar el tamaño de las posiciones hasta que nuestra estrategia pase un Drawdown similar al Máximo Drawdown estimado en nuestros backtests?
- ¿Se puede predecir si nuestra estrategia seguirá siendo ganadora o no simplemente analizando el comportamiento del Máximo Drawdown a lo largo del tiempo?
Si les apetece, podemos debatir sobre todas estas cuestiones en el hilo que acabo de abrir en el Foro 😉
Saludos,
X-Trader



