En la última kedada de X-Trader.net presenté una aplicación del filtro de Kalman al trading de pares. Para los que no pudisteis asistir al evento, aquí tenéis un resumen de mi ponencia junto con el código en R.
¿Qué es el Filtro de Kalman?
El filtro de Kalman es un algoritmo desarrollado por Rudolf E. Kalman en 1960 que sirve para poder identificar el estado oculto (no medible) de un sistema dinámico lineal, incluso cuando el sistema está sometido a ruido blanco aditivo. Si bien puede parecer que se trata de un invento de algún matemático loco que no tiene aplicación práctica, lo cierto es que resulta fundamental para muchas de las tecnologías actuales, siendo la base de la mayor parte de tecnologías de guiado, navegación y control de vehículos terrestres y espaciales (de hecho la primera aplicación del filtro de Kalman fue el guiado de la misión Apollo XII), aunque también se utiliza en otros campos como el procesado de señales y la econometría.
Las matemáticas que hay detrás son bastante complejas aunque en este tutorial de Bzarg podéis encontrar una explicación más o menos intuitiva de su funcionamiento. En cualquier caso, la idea básica es que tratamos de estimar la verdadera situación de un sistema que se encuentra sometido a ruido (esto es, que su comportamiento presenta oscilaciones aleatorias), aprovechando para ello toda la información pasada, tanto de datos del sistema como de los errores previos. La ventaja del filtro es que además no requiere de una ventana de datos predefinida como sucede con otras técnicas estadísticas sino que el propio algoritmo se va ajustando a medida que entran nuevas observaciones, siguiendo un esquema similar a este:
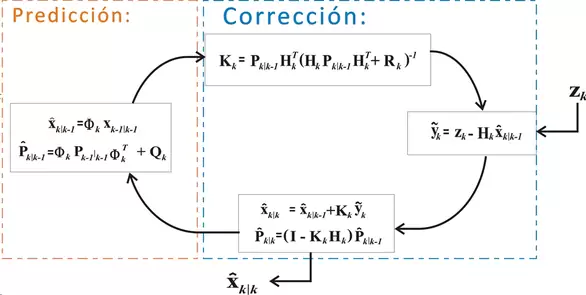
Aplicando el Filtro de Kalman al Trading
Si bien podemos pensar en múltiples aplicaciones del filtro al trading, lo más habitual es usarlo para calcular de forma dinámica el ratio de cobertura para un spread entre dos activos. La idea consiste en considerar el ratio de cobertura como una variable oculta no observable que tratamos de estimar a partir de observaciones que contienen ruido (precios de los activos).
Para que se entienda mejor todo el proceso, vamos a realizar un ejemplo utilizando las series de precios diarios de BBVA y Santander entre 2010 y 2018. Usando R cargamos los datos y vemos qué aspecto tienen:
df <- xts(read.zoo(«bancos.csv», format=»%Y%m%d», sep=»,», header=TRUE))
plot(df, legend.loc=1)
scatterplot(df$BBVA ~ df$SAN, data=df$BBVA, ellipse=TRUE)
El comportamiento de las acciones y el aspecto de su gráfico de dispersión son los siguientes:
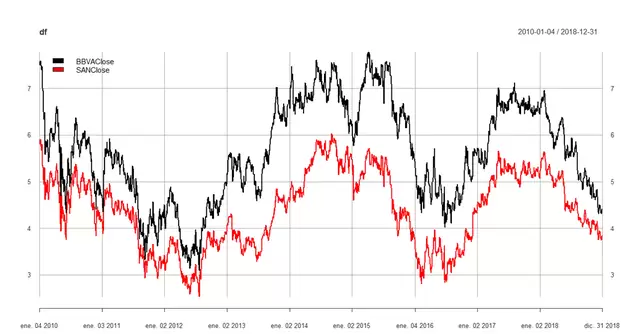
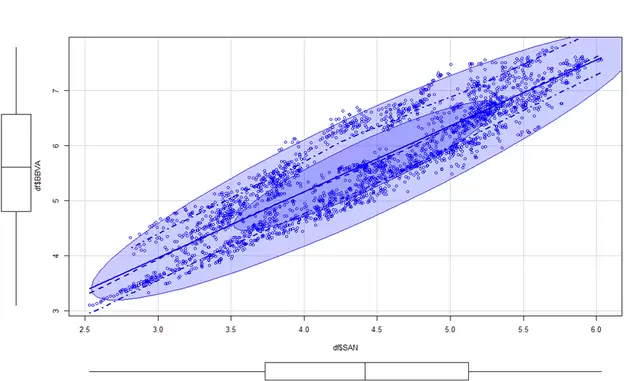
Está claro que existe relación entre ambos activos y que probablemente exista una relación de equiibrio de largo plazo entre los dos. Para confirmarlo realizamos un test ADF para verificar la presencia de cointegración. El código sería el siguiente:
summary(ur.df(df$BBVA, type=»drift», lags=1))
summary(ur.df(df$SAN, type=»drift», lags=1))

Los resultados que se obtiene indican presencia de raíz unitaria por lo que calculamos rendimientos logarítmicos y repetimos el test:
df$BBVAlogreturn[is.na(df$BBVAlogreturn)] <- 0
summary(ur.df(df$BBVAlogreturn, type=»drift», lags=1))
df$SANlogreturn<-diff(log(df$SAN))
df$SANlogreturn[is.na(df$SANlogreturn)] <- 0
summary(ur.df(df$SANlogreturn, type=»drift», lags=1))

Los resultados obtenidos confirman que ya no hay raíces unitarias por lo que confirmamos que las series en niveles son integradas de orden I(0). Ahora que sabemos que las series son cointegradas, ¿podemos estimar el valor del parámetro que relaciona a ambos activos en el equilibrio? Aquí es donde entra en juego el filtro de Kalman: dado que la trayectoria de equilibrio del spread se ve afectada por el ruido del mercado, con el filtro vamos a poder estimar en todo momento dónde debería estar el parámetro que rige dicha relación teniendo en cuenta el error que induce el ruido en los precios.
El código para obtener el valor de la beta de dicha relación de forma dinámica es el siguiente:
x <- df[, assets[1]]
y <- df[, assets[2]]
x$int <- rep(1, nrow(x))
delta <- 0.0001
Vw <- delta/(1-delta)*diag(2)
Ve <- 0.001
R <- matrix(rep(0, 4), nrow=2)
P <- matrix(rep(0, 4), nrow=2)
beta <- matrix(rep(0, nrow(y)*2), ncol=2)
y_est <- rep(0, nrow(y))
e <- rep(0, nrow(y))
Q <- rep(0, nrow(y))
if(i > 1) { beta[i, ] <- beta[i-1, ] # state transition
R <- P + Vw } # state cov prediction
y_est[i] <- x[i, ] %*% beta[i, ] # measurement prediction
Q[i] <- x[i, ] %*% R %*% t(x[i, ]) + Ve # measurement variance predicton
# error between observation of y and prediction
e[i] <- y[i] – y_est[i]
K <- R %*% t(x[i, ]) / Q[i] # Kalman gain
# state update
beta[i, ] <- beta[i, ] + K * e[i]
P = R – K %*% x[i, ] %*% R
}
Una vez ejecutado el bucle anterior podemos graficar la evolución de las betas:
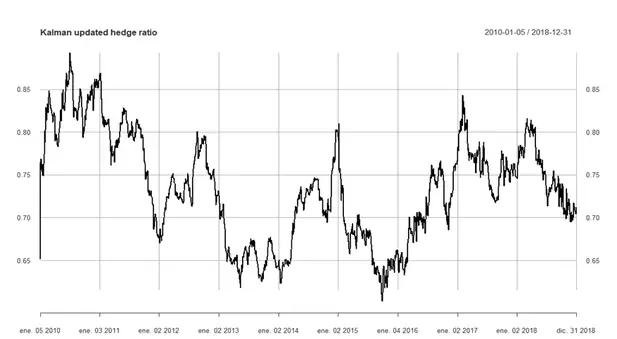
Como podemos ver, la oscilación de la beta es importante situándose en torno a las 0.85-0.87 acciones de BBVA por cada acción de SAN en 2010 a un mínimo en 0.62 a finales de 2015. Como podemos ver, el ratio de cobertura va variando de forma importante a lo largo del tiempo.
Ahora que tenemos este resultado, ¿podemos convertirlo de alguna manera en una estrategia de trading? Por supuesto, gracias a lo que explica Ernest Chan en su más que recomendable Algorithmic Trading. Basta simplemente con analizar los errores de predicción cometidos por el filtro y aprovecharlos para entrar y salir en el spread. Si representamos dichos errores y aplicamos una bandas de dos desviaciones típicas tenemos que:
e <- xts(e, order.by=index(df))
sqrtQ <- xts(sqrt(Q), order.by=index(df))
signals <- merge(e, 2*sqrtQ, -2*sqrtQ)
colnames(signals) <- c(«e», «sqrtQ», «negsqrtQ»)
plot(signals[5:length(index(signals))], ylab=’e’, main = ‘Trade signals at two standard deviations’, col=c(‘blue’, ‘black’, ‘black’), lwd=c(1,2,2))
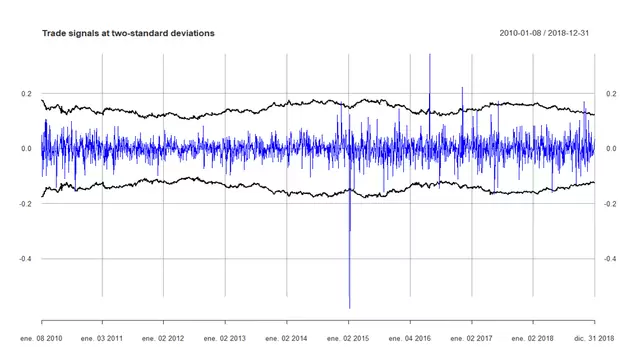
# vectorised backtest
sig <- ifelse((signals[1:length(index(signals))]$e > signals[1:length(index(signals))]$sqrtQ) & (lag.xts(signals$e, 1) < lag.xts(signals$sqrtQ, 1)), -1,
ifelse((signals[1:length(index(signals))]$e < signals[1:length(index(signals))]$negsqrtQ) & (lag.xts(signals$e, 1) > lag.xts(signals$negsqrtQ, 1)), 1, 0))
colnames(sig) <- «sig»
sig[sig == 0] <- NA
sig <- na.locf(sig)
sig <- diff(sig)/2
plot(sig)
El resultado es el siguiente:
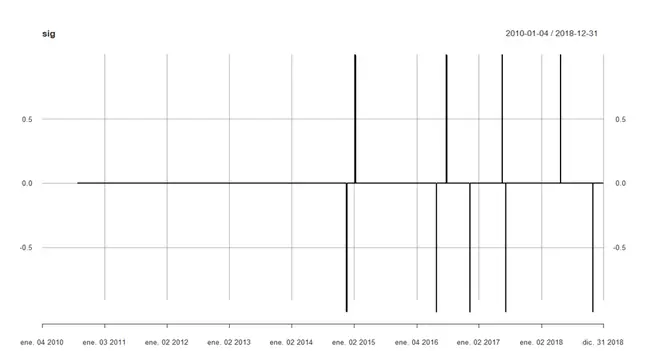
Como podemos ver muy pocas señales, por lo que no cabe esperar grandes beneficios tampoco. Calculamos cuanto habríamos ganado con un sistema de operativa continua que compra cuando los errores se salen debajo de la banda inferior y vende cuando se salen por la de arriba:
sim <- merge(lag.xts(sig,1), beta[, 1], x[, 1], y)
colnames(sim) <- c(«sig», «hedge», assets[1], assets[2])
sim$posX <- sim$sig * -1000 * sim$hedge
sim$posY <- sim$sig * 1000
sim$posX[sim$posX == 0] <- NA
sim$posX <- na.locf(sim$posX)
sim$posY[sim$posY == 0] <- NA
sim$posY <- na.locf(sim$posY)
pnlX <- sim$posX * diff(sim[, assets[1]])
pnlY <- sim$posY * diff(sim[, assets[2]])
pnl <- pnlX + pnlY
plot(cumsum(na.omit(pnl)), main=»Cumulative PnL, $»)
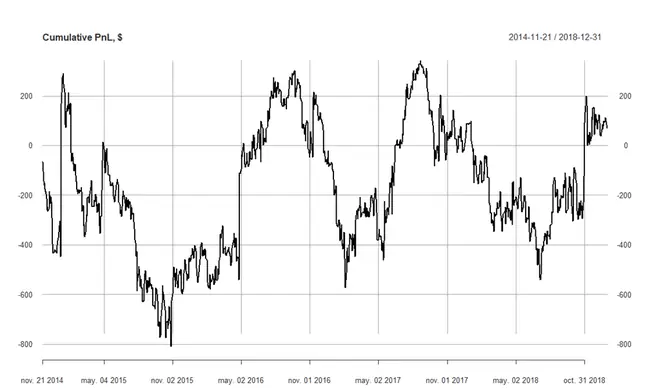
Veamos qué pasa si estrechamos las bandas un poco para generar más señales de trading. Repitiendo los cálculos con una desviación típica obtenemos los siguientes resultados:
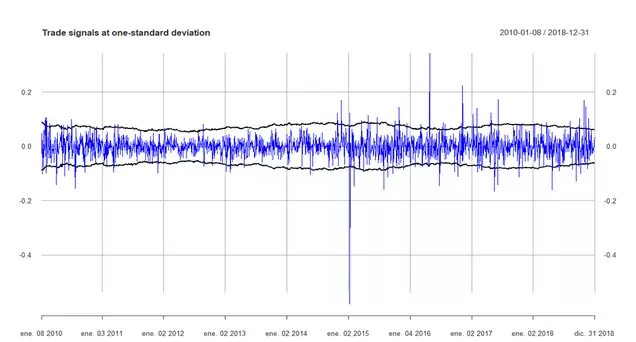
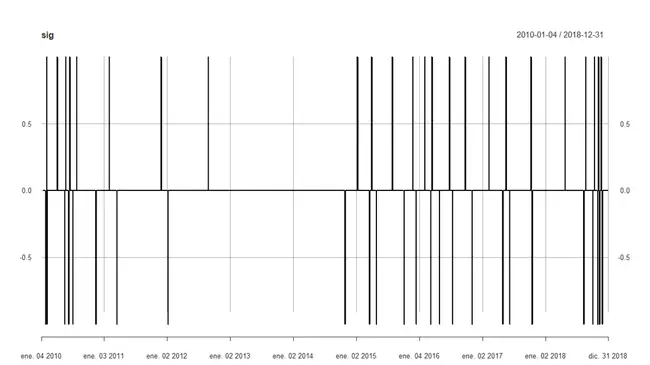
Si hacemos un backtest con esas señales podemos ver que los resultados ahora tienen mejor pinta, obteniendo una curva de beneficios bastante prometedora (aunque posiblemente le faltaría introducir un filtro para rematar la faena):
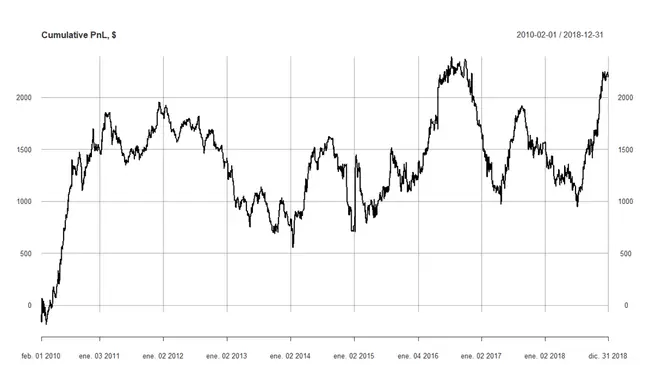
Conclusión
En este artículo hemos visto qué es filtro de Kalman y cómo podemos utilizarlo para estimar de forma dinámica la beta que relaciona dos activos en un spread, generando señales de compra y venta en función de las desviaciones de los errores de predicción, obteniendo resultados bastante prometedores. Si les ha gustado lo que hemos visto en este artículo, les dejo algunas líneas de investigación sobre las que trabajar sobre esta base:
- Trabajar la estrategia usando rendimientos logarítmicos en lugar de las series de precios en niveles.
- Desarrollar un método de selección del múltiplo de desviaciones típicas óptimo.
- El filtro de Kalman es una versión básica y lineal de lo que se conoce como modelos de espacio-estado, pero en algunos artículos académicos se han obtenido buenos resultados en la predicción de la volatilidad usando modelos de espacio-estado no lineales.
Saludos,
X-Trader