A petición de Rafa7 en el Foro, os traduzco este interesante artículo de Mike Bryant sobre la creación de series de precios sinteticas para evaluar y mejorar sistemas de trading.
Uno de los problemas que a menudo nos encontramos cuando desarrollamos y probamos sistemas de trading es la insuficiencia de datos para producir resultados fiables. Debemos tener en cuenta que, en general, los resultados de las pruebas de un sistema son más fiables cuantos más datos utilicemos. En su libro Beyond Technical Analysis, Tushar Chande aborda este problema mostrando cómo generar datos de precios sintéticos utilizando un método denominado mezclado de datos.
La idea básica de este método es comenzar con una serie de precios reales y tomar una muestra al azar de esos datos para crear una serie de precios sintética. Sin embargo, en lugar de muestrear directamente a los precios, lo que haremos será muestrear a partir de las variaciones de precios. Veamos la siguiente hoja de cálculo:
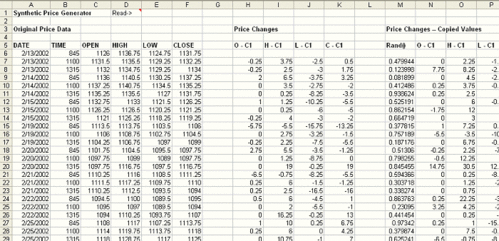
En ella, las seis primeras columnas contienen los datos de precios originales. Por su parte, las columnas H – K convierten los datos de precios en variaciones, restando el cierre de la barra anterior. Por ejemplo, el nuevo valor de apertura se obtiene restando a la apertura el cierre anterior, el máximo se convierte en el máximo menos el cierre anterior, etc. Es necesario trabajar con los cambios de precios en lugar de los precios absolutos con el fin de preservar los cambios de precios de barra a barra.
Tras calcular todos los cambios de precios, el siguiente paso es seleccionar al azar el orden de dichas variaciones. En este caso vamos a aplicar un método ligeramente diferente del propuesto por Chande, que utiliza muestreo aleatorio con reemplazamiento. En el muestreo con reemplazamiento, se seleccionan aleatoriamente las filas que contienen las variaciones de precios y se utilizan para construir los nuevos precios. El problema de hacer esto es que podemos coger la misma fila más de una vez. En su lugar vamos a utilizar un muestreo aleatorio sin reemplazamiento en el que seleccionaremos cada fila solo una vez.
Para hacer esto en la hoja de cálculo, copiamos las columnas que contienen los cambios de precios (H – K) y pegamos solo los valores (no las fórmulas) en las nuevas columnas (N – Q) como se puede ver en la siguiente figura. A continuación, añadimos una columna adicional (M) a la izquierda de las columnas copiadas para contener números aleatorios.
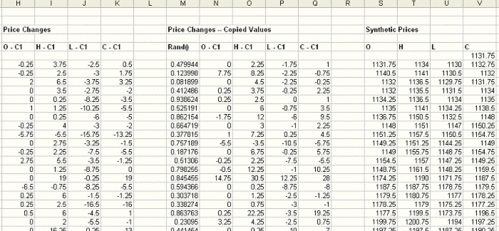
Los números aleatorios se pueden producir en Excel utilizando la función ALEATORIO(). Ahora que tenemos los cambios de precios y la columna de números aleatorios, seleccionamos las cuatro columnas de los cambios de precios, además de la columna de números aleatorios (M – Q) y ordenamos las columnas (utilizando el comando Ordenar del menú Ordenar y Filtrar) según la columna de números aleatorios (M). Esto nos permite hacer aleatorio el orden de los cambios de precios. Observe que ordenamos las columnas de los cambios de precios en conjunto, por lo que los datos de cada barra permanecen juntos.
Por último, los precios sintéticos se generan mediante la suma de los cambios en los precios a la serie original. Por ejemplo, la diferencia entre apertura y cierre se suma al precio de cierre anterior para crear el precio de apertura sintético. Para poder iniciar el proceso de generación de precios debemos tomar un precio de cierre de referencia, que se utilizará para asignar el valor a la primera fila. En la figura anterior, el precio de cierre de referencia es 1.131,75, que aparece como primer valor de la columna de cierres sintéticos (columna V). Las filas subsiguientes se crean mediante la suma de los cambios de precios de cada fila a los valores de la fila anterior. De esta manera, cada barra de precios depende la barra anterior.
Como muestra del tipo de datos que se generan con este procedimiento, veamos los siguientes gráficos: el primero es el gráfico original, mientras que los tres siguientes contienen tres conjuntos diferentes de precios sintéticos generados al azar siguiendo el procedimiento descrito.
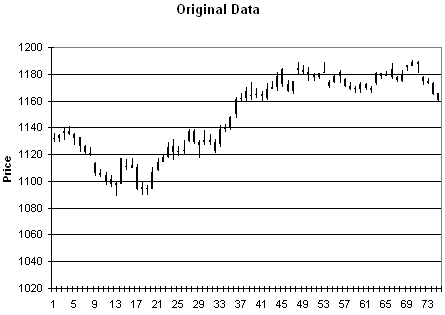
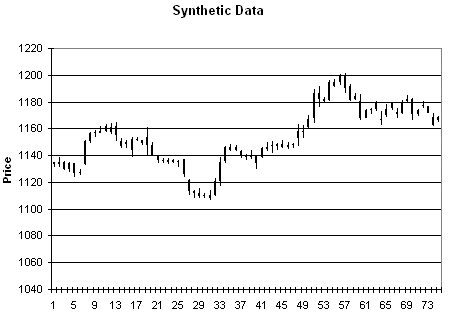
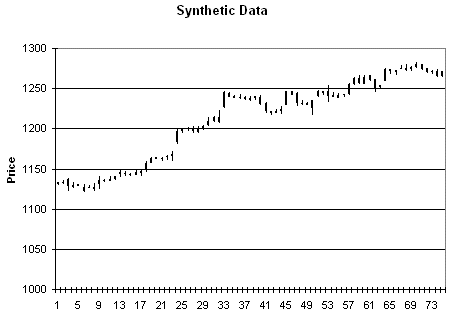
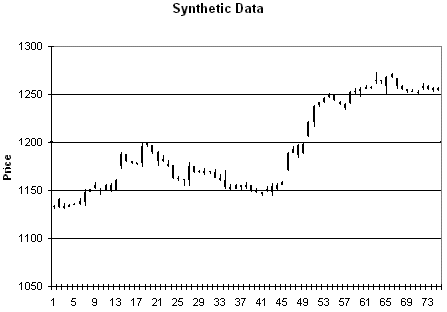
Si queréis jugar un poco con la hoja de cálculo podéis descargarla haciendo click aquí.
El método aquí presentado permite conservar no sólo los cambios en los precios, también las relaciones de precios dentro de cada barra. Se trata básicamente de hacer aleatorio el orden de las barras, pero manteniendo cada barra igual. La única característica del precio que está siendo alterada es el orden de las barras. La ventaja de este enfoque es que conserva buena parte de la información de la serie de precios mientras se generan diferentes formaciones de precios en las nuevas series sintéticas. Sin embargo, si Vd. tiene un sistema de trading que se basa en patrones de precios o métodos que dependen de un orden específico de las barras de precios, no hay razón para pensar que el sistema seguirá funcionando cuando se pruebe sobre los datos sintéticos. Por ejemplo, si hemos detectado que cuatro cierres alcistas seguidos es una señal de compra válida, no deberíamos esperar encontrar ese resultado en una serie de precios sintética. Si este patrón de precios en particular es útil, es porque posiblemente capta cierta tendencia del mercado no aleatoria, como una respuesta psicológica a una fuerte tendencia a corto plazo. Si aplicamos el método de muestreo aleatorio a los cambios de precios, perderemos ese patrón en la serie de precios sintética.
Además, mientras que la serie de precios sintética puede parecer muy diferente de la serie de precios original, dicha serie aún contiene la misma distribución estadística de los cambios. Con el tiempo, los mercados cambian. Una característica que puede cambiar es la distribución de los cambios de precios. En ese caso, debemos tener en cuenta que los datos sintéticos como los descritos aquí no lo tendrán en cuenta.
Aplicaciones de los Precios Sintéticos
Teniendo en cuenta los puntos que acabamos de ver, vamos a ver dos aplicaciones de los datos de precios sintéticos. La primera aplicación es la recomendada por Chande; es decir, utilizar datos sintéticos para las pruebas del sistema. Chande describe este uso como una verdadera prueba fuera de la muestra. Ciertamente, un sistema que funciona bien en datos de precios sintéticos es más robusto que uno que sólo va bien sobre datos históricos. Esto implica que el sistema es insensible al muestreo aplicado para generar datos sintéticos. En términos generales, cuanto menos sensible sea un sistema a cambios en las características del mercado, mejor. Por ejemplo, si yo tuviera un sistema que fuera insensible a la volatilidad de los precios, sería mejor que un sistema con un rendimiento similar que pudiera fallar por cambios en la volatilidad del mercado. Un sistema que se sostiene bien cuando se reordenan los cambios de precios, al igual que con una serie de precios sintéticos, es mejor que un sistema que se derrumba al probarlo sobre datos sintéticos. Sin embargo, no hay garantía de que un sistema que funciona bien con datos sintéticos seguirá haciéndolo en el futuro. Como se señaló anteriormente, la distribución de las variaciones de precios podría variar con el paso de tiempo o incluso cambiar de repente, algo que los precios sintéticos obtenidos no pueden reflejar.
Suponiendo que estamos utilizando un sistema que funciona bien con datos sintéticos, podríamos ampliar el enfoque de Chande. En lugar de simplemente probar un sistema con datos sintéticos, ¿por qué no crear una serie muy larga de precios sintéticos y optimizar los valores de los parámetros del sistema sobre esta nueva serie? ¿Cómo de larga debe ser la nueva serie? Debemos tener en cuenta que cuanto mayor sea el número de operaciones obtenidas al aplicar el sistema, mejor. Si podemos crear una serie de precios sintética que genere 500 operaciones del sistema, ello sería mejor para la optimización que uno con sólo 100 operaciones. Después de la optimización, pruebe el sistema con valores de los parámetros optimizados «fuera de la muestra» sobre datos de precios reales. Para realizar mejores pruebas con datos fuera de muestra, divida los datos históricos originales en dos segmentos. Utilice el primer segmento para crear una serie larga de precios sintéticos que utilizaremos para la optimización. Guarde el segundo segmento de datos históricos para realizar la verdadera prueba fuera de muestra con el sistema optimizado. Esto tiene las siguientes ventajas:
- Estaremos optimizando a través de un amplio histórico de precios que genera un gran número de operaciones.
- Los datos incluyen patrones aleatorios por lo que los valores de los parámetros resultantes no estarán ajustados a un pequeño número de patrones históricos de precios que puede que nunca se repitan.
- Al guardar los datos históricos reales para las pruebas fuera de la muestra, los resultados finales de la prueba le dará confianza de que el sistema es capaz de realizar bien en los datos «reales».
En principio, una de las ventajas de utilizar precios sintéticos es que se pueden crear series arbitrariamente largas. Sin embargo, en la práctica el uso de la hoja de cálculo descrito anteriormente puede ser un poco complicado. He aquí una manera de hacerlo de forma sencilla. Copie los datos en las columnas de cambios de precios (N – Q) y pegue los datos directamente debajo de los números existentes en las mismas columnas, con ello duplicará la longitud de las columnas. Repita el proceso tantas veces como sea necesario para obtener la longitud que desee. A continuación, rellene hacia abajo la columna de números aleatorios (M) y las columnas de precios sintéticos (S – V). A continuación ordene las columnas de cambios de precios (N – Q) por la columna de números aleatorios (M). Con esto hacemos aleatorios solo los cambios de precios y produciremos precios sintéticos en las columnas S – V. El único problema es que tendremos que asignar fechas/horas a los precios con el fin de crear un histórico completo. Si los datos son barras diarias, de manera que cada barra tiene una fecha consecutiva diferente, esto es relativamente sencillo. Para ello convertiremos las fechas a números formateando la columna de la fecha como “texto”. Entonces incrementaremos cada valor de fecha, que ahora es un número, en una unidad cada vez a partir de la última fila de la que tengamos información disponible en estos momentos. Por ejemplo, si la última fila para la que tenemos fechas es la 546 y la fecha es 21/11/2005, entonces sería convertir esta fecha en un número (en este caso, es 38.677) por el formato de la celda como texto. Luego se establece la celda de fecha para la siguiente fila como A546 + 1 (suponiendo que las fechas están en la columna A). La fecha para la siguiente fila sería A547 + 1, etc. Luego volvemos a dar formato a las celdas como fechas. Los datos intradía pueden requerir un poco más de trabajo debido a que varias filas de datos tendrán la misma fecha, pero la idea es la misma.
La segunda aplicación de los datos de precios sintéticos es la prueba de patrones de precios. Anteriormente dijimos que si su sistema de trading se basa en un patrón de precios, entonces es probable que se pierda ese patrón cuando aplicamos el muestreo aleatorio para generar precios sintéticos. En ese caso, nuestro objetivo no es llegar a un sistema que sea insensible a los patrones de cambio de precio, como lo sería si estuviéramos usando datos sintéticos para optimizar nuestro sistema. Todo lo contrario: hemos encontrado un patrón de precios que creemos que representa una especie de fenómeno de mercado no aleatorio, y nuestro objetivo es determinar si el patrón tiene alguna validez.
Supongamos, por ejemplo, que hemos encontrado un patrón que parece predecir que el mercado subirá cinco días más tarde, con un 60% de acierto. Necesitamos saber si el 60% de precisión es significativa o si simplemente acertamos por azar. Si el azar es el que produce ese nivel de acierto, entonces nuestro modelo no es significativo. Aquí es donde los datos de precios sintéticos entran en juego: debido a que estos se generan mediante muestreo aleatorio de los cambios de precios, podemos buscar nuestro patrón en los datos sintéticos para determinar la exactitud de la pauta en los precios aleatorios. Para que nuestro patrón de precios tenga sentido y no sólo sea producto de la casualidad, el patrón debe tener (en términos estadísticos) una mayor precisión en los datos reales que en la mayor parte de los datos de precios sintéticos.
Como ejemplo, vamos a considerar un modelo para el futuro E-mini sobre S&P 500 en barras de 135 minutos en el histórico comprendido entre el 13/02/2002 y el 21/11/2005. Las barras de 135 minutos dividen la sesión uniformemente en tres partes (mañana, mediodía y tarde).
El patrón de precios que vamos a analizar es el siguiente:
– El menor mínimo de las últimas 20 barras se encuentra dentro de las últimas 5 barras
– El rango de la barra es menor que promedio de rangos de las últimas tres barras
– El cierre es mayor que el de la barra anterior.
– El cierre es mayor que la media de los cierres de las últimas 180 barras
Evaluamos este patrón mediante el cálculo de la probabilidad de que el mercado haya subido cinco días después.
Resultados
En los datos originales:
El 65,4% del tiempo (34 de 52 patrones), el cierre fue mayor que el actual 5 días más tarde.
En los datos sintéticos:
Series Probabilidad
1 55.9
2 50.0
3 50.0
4 40.8
5 49.1
6 49.1
7 50.0
8 50.0
9 42.9
10 40.8
Cada serie constaba de una serie de precios sintéticos diferente creada a partir de los datos originales. Durante toda la serie 10, la probabilidad media es de 47.86 +/- 4.83%. En otras palabras, la probabilidad promedio de las 10 series es de 47.86% y la desviación estándar es de 4.83%. Lo ideal sería tener unas 30 series para asegurar que la distribución es estadísticamente válida, pero a fin de simplificar el ejemplo, vamos a suponer que con 10 es suficiente.
En general, el 99.9% de los datos distribuidos normalmente tienen menos de tres desviaciones estándar por encima de la media. En este caso, tres desviaciones estándar por encima de la media es 47.86 + 3 x 4.83 = 62.4%. En otras palabras, el 99.9% de los resultados de la serie de precios sintéticos será de menos de 62,4%. Dado que el patrón funciona en el 65.4% del tiempo utilizando datos reales, la precisión de nuestra estructura de precios es mayor que en el 99.9% de los valores de precisión calculados a partir de los datos sintéticos, lo que implica que la probabilidad obtenida no se debe a la casualidad, sino a algún otro fenómeno. Esto nos debe dar cierta seguridad de que el patrón detectado en los precios está capturando algo más que ruido.
Los dos usos de los datos sintéticos descritos aquí para la evaluación de los sistemas de trading son bastante diferentes entre sí. En un caso, estamos probando u optimizando nuestro sistema de trading en los precios sintéticos con la expectativa de que nuestro sistema tenga un buen rendimiento incluso en los datos sintéticos generados aleatoriamente. En el otro caso, esperamos que nuestro patrón de precios sólo funcione bien en los datos originales. Es evidente que la forma en que usemos los datos sintéticos depende del tipo de sistema que estemos analizando. Siempre que tengamos esto en mente, los datos de precios sintéticos podrán ser una herramienta útil para ayudar a desarrollar y analizar sus sistemas de trading.
Saludos,
X-Trader