Si algo ha demostrado la reciente crisis financiera es que el enfoque tradicional de la teoría de carteras tiene importantes limitaciones, lo que ha contribuído a que aumente el interés por medidas más avanzadas de rentabilidad en términos de riesgo que el ratio de Sharpe. Como seguramente ya saben, el principal defecto de este ratio es el uso de la desviación típica en el denominador de su fórmula ya que, por un lado si la distribución de los rendimientos producidos por una estrategia tiene colas anchas, su desviación típica tiende a infinito por lo que el ratio de Sharpe queda invalidado; asimismo no existe un punto de acuerdo sobre el tamaño muestral que debe utilizarse para calcularla por lo que una gestora puede, por ejemplo, «maquillar» fácilmente sus resultados en términos de Sharpe eligiendo el valor de la desviación típica que más le convenga, aclarando después en la letra pequeña cuál es el tamaño muestral empleado.
Los ratios que vamos a ver a continuación provienen del mundo de los hedge funds y de los CTAs, donde son utilizados desde hace tiempo de forma regular para evaluar el resultado de su gestión, si bien nada nos impide aplicarlos también al mundo de los sistemas de trading.
Ratio de Sortino
Creado en 1986 por Brian Rom, el creador de la compañía Investment Technologies, en 1986 junto con Frank A. Sortino, director del Pension Research Institute de San Francisco, la formulación del ratio de Sortino es similar en apariencia a la del ratio de Sharpe, si bien en su cálculo penaliza a aquellos rendimientos cuyo valor no supere un determinado objetivo de rentabilidad; asimismo la medida de volatilidad utilizada para corregir el ratio por riesgo no tiene nada que ver con la tradicional desviación típica, utilizándose en su lugar una medida de dispersión de los rendimientos negativos, algo que ha sido bastante criticado por diversos autores.
Matemáticamente el ratio de Sortino se expresa como:
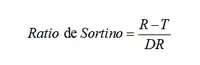
Donde R es el rendimiento de la estrategia, T es, dependiendo de la fuente, nuestro objetivo mínimo de rentabilidad o el tipo de interés de un activo libre de riesgo, y DR es la raíz cuadrada de la semivarianza de los rendimientos negativos, la cual se calcula como:
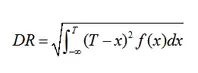
donde f() es la función de densidad de los rendimientos. Así, el ratio puede interpretarse como el exceso de rendimiento por encima de un determinado objetivo por unidad de riesgo a la baja. Lógicamente cuanto mayor sea el valor del ratio mejor será la estrategia en términos del riesgo asumido.
Ratio Calmar
Aunque en España es prácticamente desconocido, el ratio Calmar es muy utilizado actualmente en la industria financiera. Apareció publicado por primera vez en 1991 en la revista Futures y fue desarrollado por Terry W. Young; precisamente su nombre procede del acrónimo formado a partir del nombre de la newsletter que enviaba su autor a sus clientes, denominada CALifornia Managed Accounts Report. El ratio Calmar se define como el cociente entre la rentabilidad anualizada del sistema y su máximo drawdown en valor absoluto. Es decir:
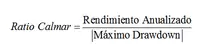
Donde la rentabilidad y el máximo drawdown se suelen obtener a partir de los datos de los últimos 36 meses. Nuevamente cuanto mayor sea el valor del ratio, mejor será la estrategia si comparamos su rentabilidad frente al riesgo asumido.
A modo de anécdota, cabe señalar que si bien el ratio Calmar es el más utilizado, antes de la aparición de este ratio ya existían otros muy similares tales como el ratio Sterling y el ratio MAR; incluso el nombre de éste último también procede de un acrónimo, el del título de la newsletter Managed Account Reports fundada en 1979 por Leon Rose. En todo caso, la formulación y los resultados obtenidos con estos ratios son muy similares a los del ratio Calmar.
Ratio Omega
Creado por Keating y Shadwick en 2002, el ratio Omega utiliza la función de distribución acumulada F(x) de los rendimientos obtenidos con la estrategia y un umbral L, a partir del cual se delimitan las áreas de ganancia y pérdidas esperadas. Dicho umbral puede ser simplemente cero o un objetivo de beneficio anual que tengamos. Posiblemente con un gráfico se entienda mejor la idea:
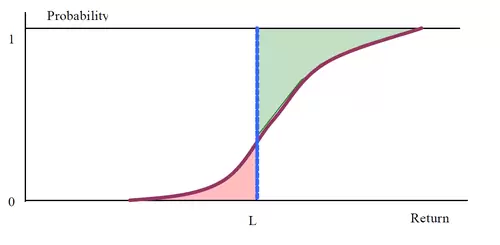
El ratio Omega es simplemente el cociente entre las dos áreas coloreadas en el gráfico anterior tal que:
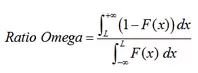
Cuanto mayor sea este ratio mejor será el sistema ya que nos estará indicando que existe mayor densidad a la derecha del umbral que a su izquierda.
Saludos,
X-Trader
Referencias
Keating, C. y Shadwick, W.F. (2002), «A Universal Performance Measure», Working Paper, The Finance Development Centre
Sortino, F. A. y van der Meer, R (1991), «Downside Risk», The Journal of Portfolio Management 17(4)
Young, T. W. (1991), «Calmar Ratio: A Smoother Tool», Futures Magazine