Nadie cuestiona que las simulaciones de Montecarlo son una excelente herramienta para determinar los riesgos y expectativas de beneficio de cualquier producto financiero que disponga de series históricas. Sin embargo, no todos los métodos de simulación son adecuados para cualquier producto ni ofrecen respuesta a las mismas cuestiones clave.
Hoy seguiremos hablando de ello en la segunda y última entrega de esta serie. Le invitamos a que lea el primer artículo publicado en el pasado número de Hispatrading Magazine.
MÉTODO III: AÑADIR RUIDO A LAS COTIZACIONES HISTÓRICAS
El empleo de simulaciones de Montecarlo para el análisis de series temporales es una práctica habitual en el ámbito de las finanzas cuantitativas. Existe también una amplísima bibliografía académica sobre el uso de modelos estocásticos en el estudio de dinámicas de los mercados así como para predecir la evolución de los precios.
Los modelos más sencillos (véase M. Pažický: “Stock Price Simulation Using Bootstrap and Monte Carlo”) se basan en la generación de números aleatorios para simular la variabilidad de los precios. Por ejemplo, aquellos que asumen el movimiento Browniano (GBM) parten de este presupuesto: los precios se acomodan a una distribución log-normal con una media conocida y una desviación estándar multiplicada por un componente aleatorio.
De este modo, descomponen el retorno (r) entre dos intervalos dados, en drift (deriva de los precios) + volatilidad, siendo:
Drift = µ-1/2 σ2
Volatilidad = σ*Z[Aleatorio (0;1)]
Es decir, para dirección del retorno se toma el retorno medio de la serie menos la mitad de su varianza y, para la volatilidad, la desviación estándar de los precios multiplicada por un coeficiente aleatorio. De este modo:
r = (µ-1/2σ2)+ σ*Z[Aleatorio (0;1)]
y
Precio Actual = Precio Anterior * e((µ-1/2σ2)+ σ*Z[Aleatorio (0;1)])
Aleatorizando el valor de Z podemos construir una simulación de Montecarlo con el número de iteraciones deseadas.
Otros modelos más sofisticados utilizan estimaciones no lineales de los precios, ecuaciones diferenciales estocásticas (métodos de la familia ARCH-GARCH) o técnicas de análisis multivariado de alta dimensionalidad. También hay modelos basados en lógica difusa y redes neuronales (E. Shavandi y H. Ghanbari: “Integration of Genetic Fuzzy Systems and Artificial Neural Networks for Stock Price Forecasting”, 2010) o variantes de método Markov-Fourier en combinación con el Grey Model (Y. Hsu, M Liu, J. Yeh y H. Hung: “Forecasting the Turning Time of Stock Market Based on Markov–Fourier Grey Model”, 2009).
Otra alternativa es construir series parcialmente sintéticas derivadas de la serie original. Para ello se utilizan técnicas de remuestreo o bootstrapping que permiten aleatorizar la secuencia de precios y obtener un conjunto de n series alternativas en las que evaluar la estrategia. La ventaja de este método es que se conservan las propiedades estadísticas de la distribución, si bien se rompen las dependencias seriales, los efectos de tipo estacional y las correlaciones entre activos del mismo grupo o mercado. En todo existen técnicas que resuelven parcialmente estos inconvenientes. Cuando se utilizan grandes volúmenes de datos o series intradiarias este método se complica aún más ya que hay que garantizar la fuerte correlación entre amplitud de rango y distribución del volumen a lo largo de la sesión.
Por ello, para operativa intradiaria, nos gusta el método de expansión y contracción de barras (ECB) consistente en añadir una pequeña porción de ruido aleatorio en los máximos, mínimos y cierres de cada barra.
Un método eficaz para implementar un proceso de Montecarlo añadiendo ruido a los precios debe cumplir estos tres requisitos:
- Generar cambios en el tamaño de las barras sin distorsionar las relaciones de dependencia o las propiedades de la distribución de precios de la serie original.
- Modificar dinámicamente los precios desde la plataforma; durante el backtest u optimización de la es- trategia. Esto evitará crear cientos o miles de series aleatorias fuera de la plataforma y luego importarlas como símbolos, lo que constituye un proceso tedioso y en la práctica inviable.
- Disponer en la plataforma de todas las estadísticas y ratios generados al evaluar el sistema en cada serie y poder exportarlos con facilidad.
De todas las fórmulas que hemos probado para añadir ruido a los precios nos gusta, por su simplicidad, la que se basa en aleatorizar una fracción del ATR que se suma o resta a las series O-H-L-C. Hemos probado dos variantes:
1.- Coeficiente aleatorio único:
NewClose[0] = Close[0] + Rand.Between (ATR(x)*-1, ATR(x))* coef (0,1)
Donde:
x = Número de barras del ATR. Utilizamos un valor pequeño (2-5) ya que interesa capturar la volatilidad próxima.
coef = Parámetro que determina el nivel de ruido.
Al realizar la simulación conviene probar fracciones aleatorias del ATR entre 0 y 1.
2.- Volatilidad ascendente y descendente:
Descomponemos la volatilidad en:
UpTicks =(High – Open)/ TickSize -> UpVolat= SMA(UpTicks, x)
DownTicks = (Open – Low) / TickSize -> DownVolat = SMA(DownTicks, x)
CloseTicks = Abs(Close[1]-Close[0])/TickSize -> CloseVolat (CloseTicks,x)
Calculamos los componentes aleatorios de las tres series:
HighA = Rand.Between (UpVolat*-1, UpVolat)
LowA = Rand.Between (DownVolat*-1, DownVolat)
CloseA = Rand.Between (CloseVolat*-1, CloseVolat)
Filtramos las inconsistencias:
if (High[0]+ HighA < Close[0])
NewHigh[0] = Close[0]
else
NewHigh[0] = High[0]+ HighA if (Low0] – LowA > Close[0])
NewLow[0] = Close[0]
else
NewLow[0] = Low[0]- LowA NewClose[0] = CloseA + Close[0]
Para el modelo con anclaje de barra:
NewOpen[0] = NewClose[1]
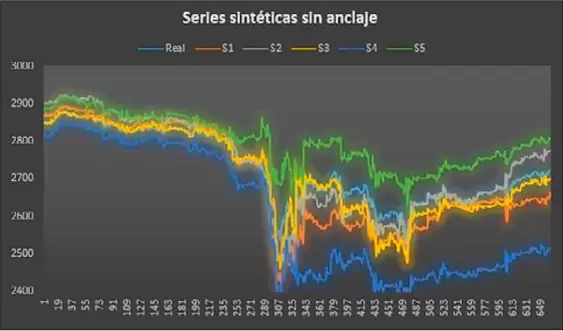
Figura 1. Series sintéticas sin anclaje
Y, para el modelo sin anclaje, se calcula la diferencia acumulada entre cierres consecutivos y se va añadiendo a la nueva serie de cierres, con lo cual los cambios en los precios son acumulativos. Para evitar que las series difieran demasiado el modelo sin anclaje se resetea cada x barras.
En la Figura 1 mostramos una simulación de series sin anclaje: estos son los modelos más básicos con los que estamos experimentando, pero se pueden crear modelos más complejos que incluyan:
- Translocación de barras próximas, que consiste en intercambiar las barras contiguas situadas en un clúster de tamaño variable. Este mecanismo se implementa en cualquiera de los anteriores modelos para generar más diversidad.
- Efectos de Cisne Negro, esto es, la generación aleatoria de barras anormalmente alcistas-bajistas (en ráfagas cortas de 1-5) cada x barras (ej. 1000).
Seguidamente mostremos los resultados de uno de estos modelos en su versión más simple. El código base sería:

Figura 2. Código base. Cálculo de la serie de cierres sintéticos.
Dependiendo de la plataforma, su implementación puede ser bastante sencilla en aquellas que permiten crear símbolos nuevos a partir de cualquier serie y algo más compleja en el resto. Por ejemplo, en NinjaTrader, además del indicador con las series sintéticas, es preciso crear un “Fill Type” personalizado si queremos que la estrategia se evalúe en las series sintéticas tanto en las entradas como en las salidas. De lo contrario solo se modificarán aleatoriamente las condiciones de entrada, mientras que los puntos de salida (Stop Loss, Profit Targets, etc.) se colocaran tomando como base el histórico original.
Las simulaciones de Montecarlo en series sintéticas permiten generar una enorme cantidad de información que no puede obtenerse con otros métodos y el tipo de análisis a realizar es muy variado, desde la determinación del DD máximo para distintos niveles de ruido hasta pruebas de robustez paramétrica en diferentes escenarios de volatilidad simulada.
Asimismo, este método se puede utilizar en combinación con el SPR descrito en el apartado anterior. La combinación de ambos nos permitirá evaluar los sistemas de trading en entornos multiescenario complejos, obteniendo resultados mucho más ricos y precisos que con los métodos de evaluación convencionales. Veamos algunos ejemplos:
1. – BMO en función del ruido: simulamos 1.000 escenarios para 3 umbrales diferentes de ruido:
- Bajo: Coeficiente aleatorio (CA) = 0,3 x ATR.
- Medio: CA = 0,6 x ATR.
- Alto: CA = 0,9 x ATR.
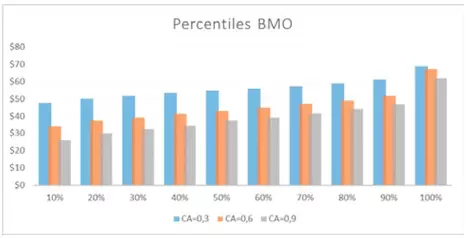
Figura 3. Percentiles BMO
2.- Nivel de ruido y beneficio acumulado: simulamos 1000 escenarios para 6 niveles diferentes de ruido y tomamos como referencia los valores mensuales de la mediana para graficar el Net Profit.
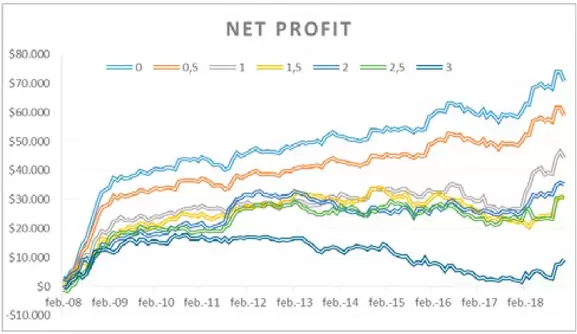
Figura 4. Net Profit
3.- Robustez paramétrica: el generador de series sintéticas nos permitirá realizar pruebas mucho más completas de robustez paramétrica que en las simulaciones de escenario único. En la imagen inferior analizamos la sensibilidad al ruido de los distintos valores de un filtro basado en el CMO.
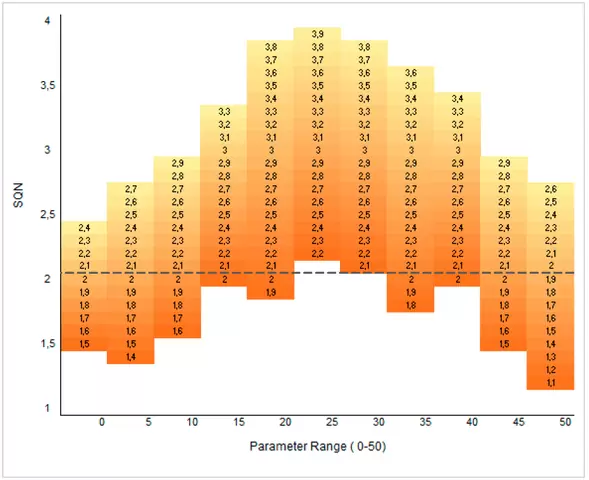
Figura 5. Parametrer Range
En definitiva, este modelo permite analizar el comportamiento de una estrategia simulando una amplia gama de variaciones en los precios. Tanto si se usa en solitario como en conjunción con el procedimiento RPR nos permitirá ir mucho más allá de las clásicas simulaciones de Montecarlo basadas en aleatorizar una secuencia de operaciones y obtener información mucho más rica y detallada.
Por otra parte, estos modelos alternativos están exentos de las principales limitaciones del método convencional. Si bien su dificultad radica en construir escenarios simulados plausibles y consecuentes con la dinámica de los mercados. Además, claro está, de que su implementación consume más tiempo y requiere, en algún caso, modificar el código de la estrategia y del optimizador.
Por último, decir que ambos métodos constituyen la base de un procedimiento de evaluación multiescenario que actualmente estamos investigando y cuya aplicación en todo tipo de estrategias resolverá muchas deficiencias de los métodos “mono-hilo” o de escenario único, contribuyendo a obtener interpretaciones más realistas de los resultados hipotéticos o de backtest de cualquier sistema algorítmico.
Artículo publicado en el número 39 de la revista Hispatrading. Regístrate en www.hispatrading.com de manera completamente gratuita para acceder a más artículos como este.






