La Transformación de Fisher

Normalmente se parte del supuesto de que los precios tiene una función de densidad gaussiana o Normal. Como ya sabrán, se trata de una función con forma de campana en la que el 68% de la probabilidad está contenida a una distancia de +/-1 desviación típica con respecto a la media. Por supuesto este supuesto sabemos que en la práctica es muy poco realista y explica en buena medida porque muchos indicadores fallan cuando el precio se mueve de forma violenta.

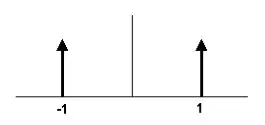
Imaginemos que el precio, en realidad, se mueve de forma similar a una onda cuadrada; si intentáramos hacer trading en base a los cruces del precio con su media móvil, siempre fallaríamos porque el precio se habría girado en el sentido contrario en el momento en que se produjera el cruce. Supongamos que la onda cuadrada sólo puede tomar valor -1 ó 1; la probabilidad asociada a cada valor entonces será del 50%, siendo la forma de su función de distribución la que se muestra en la siguiente figura, la cual como podemos apreciar es sensiblemente distinta de una Normal.

Este esquema se puede complicar incluso más: supongamos que el precio se comporta de forma similar a una onda senoidal. La función de distribución de la probabilidad de esta onda tiene una forma como la que se muestra en la siguiente figura:

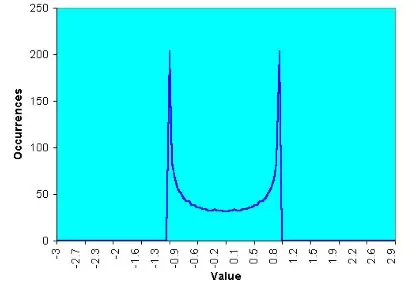
La forma de esta función de distribución es realmente curiosa, completamente diferente de la Normal, y refleja que la mayor parte de las observaciones de una onda senoidal se dan siempre cerca de sus extremos. Asimismo explica muy gráficamente porque es tan difícil predecir el comportamiento del precio en base a ciclos: porque el precio pasa la mayor parte del tiempo cerca de máximos o mínimos.

Pero, ¿se imaginan que pudiéramos transformar cualquier distribución de probabilidad en la de una Normal? La Transformación de Fisher permite hacer exactamente eso: transformar la función de densidad de cualquier onda de tal forma que la función resultante sea aproximadamente gaussiana. En particular la ecuación de la Transformación de Fisher es:

Donde:

x hace referencia a los valores de la función de distribución que queremos transformar. La única restricción es que debe cumplir x es que -1<x<1.
y es el valor resultante de la transformación.
Log es un logaritmo natural

Aplicando la transformación de Fisher a la función de distribución de la onda senoidal anterior obtenemos la transformación de Fisher que se muestra a continuación (línea roja), cuya forma es muy cercana a la de una distribución gaussiana:

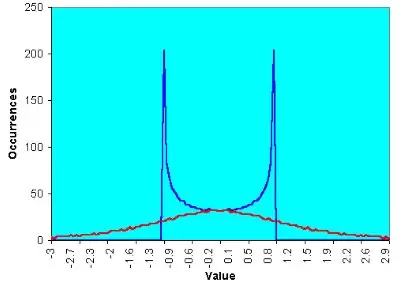
Bien, veamos ahora cómo aplicar todo esto al trading: si conseguimos normalizar el precio de tal forma que oscile entre -1 y +1 y le aplicamos al resultado la transformación de Fisher, seremos capaces de identificar de forma inequivoca y clara puntos de giro, al igual que todos al ver el gráfico anterior saben que valores por debajo de -1 o por encima de +1 es imposible que se produzcan.

Matemáticamente podemos aplicar todo esto de la siguiente forma: tomando como referencia el rango de los últimos n días, normalizamos el precio de la siguiente forma:

Z = 0.33*2*((Close – MinL)/(MaxH – MinL) – 0.5) + 0.67*Z[1];

Donde Close es el cierre, MinL es el menor mínimo de los últimos n periodos, MaxH es el mayor máximo de los últimos n periodos y Z[1] es el valor en el periodo anterior de Z (si se fijan bien en la fórmula, seguro que les recuerda bastante a la de un Estocástico suavizado con una media exponencial).

La expresión anterior en ocasiones puede generar valores que superen los límites admisibles para la transformación por lo que conviene introducir un filtro para los valores de Z tal que:

If Z > .99 then Z = .999;
If Z < -.99 then Z = -.999;

Seguidamente basta con calcular la transformación de Fisher al valor de Z aplicando una versión suavizada de la ecuación anterior:

Donde y[1] es el valor de la transformación en el periodo anterior.

Generalmente en los gráficos se suele representar el valor de la transformación junto con su retardo de un periodo para facilitar la busqueda de giros. Un ejemplo de su aplicación podemos verlo en el siguiente gráfico del GBPJPY en 1 min. Si bien su comportamiento cuando el precio está en rango no difiere demasiado del de una media móvil, cuando se produce un giro importante generalmente lo caza con un poco de retardo.

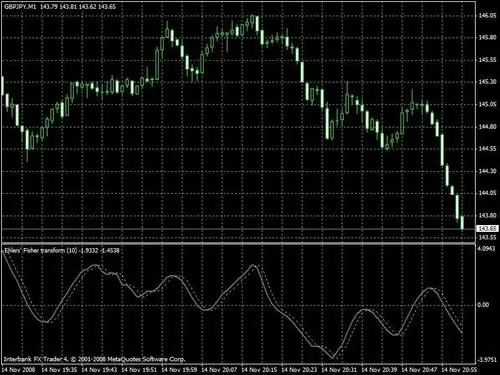
En definitiva, un estimulante camino para explorar. Por cierto, seguramente al ir leyendo el artículo alguno de Vds. habrá pensado: y no puedo aplicar esto a un Estocástico o a un RSI??? Bingo! La respuesta completa en próximos artículos.Por ahora les he dejado en el Foro el código de la transformación de Fisher para los paquetes de gráficos más extendidos.