Si bien en la Antigua Grecia, Aristóteles o Platón ya apuntaban a la posibilidad de que existieran diferentes grados de veracidad y falsedad, no será hasta la década de los sesenta cuando el ingeniero iraní nacionalizado estadounidense, Lofti A. Zadeh, acuñe el término de lógica difusa o borrosa (fuzzy logic) en el artículo Fuzzy Sets publicado en el número 8 de la revista Information and Control en 1965.
Si bien pudiera parecer que esto de la lógica difusa es un artificio matemático para decir que las cosas no son ni blancas ni negras sino gris, lo cierto es que su impacto en nuestra sociedad es mucho mayor de lo que pudiéramos esperar a priori. Así, la lógica difusa se encuentra presente en el control de complejos procesos industriales, el diseño de dispositivos artificiales de deducción automática, la construcción de artefactos electrónicos de uso doméstico y de entretenimiento o los sistemas de diagnóstico, entre otros. Fíjense si tienen cerca la lógica difusa que el popular robot aspirador Roomba o los enemigos de su juego favorito de Playstation se basan en ella.
Pero ¿qué es exactamente la lógica difusa? Para entender mejor el concepto, conviene aclarar previamente qué es la lógica clásica: se trata de aquella que impone valores deterministas de Falso y Verdadero a los enunciados. Es por tanto una lógica de tipo binario, mediante la que es posible modelizar parte de nuestro razonamiento natural aunque el resultado sea incompleto.
Sin embargo, lo cierto es que nadie afirma que una taza de leche está caliente o fría de forma categórica, incluso aunque solo utilice esa palabra. En la práctica todas nuestras afirmaciones presentan un cierto grado de veracidad pero por lo general no son absolutas. Lo habitual es que digamos que el café está “un poco frío” o que una luz es “muy brillante”. Es aquí donde entra en juego la lógica difusa, que nos va a permitir representar enunciados que de alguna manera presentan cierta vaguedad en su contenido.
Mediante la lógica difusa vamos a poder crear aproximaciones matemáticas en la resolución de ciertos tipos de problemas, produciendo resultados exactos a partir de datos imprecisos. Ello es así porque vamos a poder redefinir los grados de veracidad de los enunciados de salida conforme se refinan los de los de entrada, de ahí que los sistemas de lógica difusa aparenten incluso que realizan cierta labor de aprendizaje.
Por si no queda claro, veamos el ejemplo clásico de los “hombres altos” que propone Zadeh en su artículo: según la teoría de la lógica clásica, el conjunto “hombres altos” es un conjunto al que pertenecerían los hombres con una estatura mayor a un cierto valor, que podemos establecer en 1.80 metros, por ejemplo, y todos los hombres con una estatura inferior a este valor quedarían fuera del conjunto. Así tendríamos que un hombre que mide 1.81 metros de estatura pertenecería al conjunto de hombre altos, y en cambio un hombre que mida 1.79 metros de altura ya no pertenecería a ese conjunto. Sin embargo, no parece muy lógico decir que un hombre es alto y otro no lo es cuando su altura difiere en dos centímetros. El enfoque de la lógica difusa considera que el conjunto “hombres altos” es un conjunto que no tiene una frontera clara para pertenecer o no pertenecer a él: mediante una función que define la transición de “alto” a “no alto” se asigna a cada valor de altura un grado de pertenencia al conjunto, entre 0 y 1.
Así por ejemplo, un hombre que mida 1.79 podría pertenecer al conjunto difuso “hombres altos” con un grado 0.8 de pertenencia, uno que mida 1.81 con un grado 0.85, y uno que mida 1.50 m con un grado 0.1.
Visto desde esta perspectiva se puede considerar que la lógica clásica es un caso límite de la lógica difusa en el que se asigna un grado de pertenencia 1 a los hombres con una altura mayor o igual a 1.80 y un grado de pertenencia 0 a los que tienen una altura menor. Esta contraposición puede verse fácilmente en el siguiente esquema:
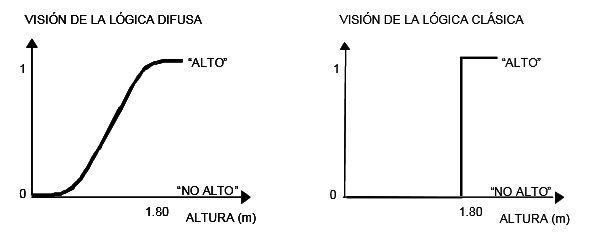
La figura anterior nos permite introducir un concepto clave en la lógica difusa: la función característica o función de membresía, la cual se define como aquella función que nos proporciona una medida del grado de similitud de un determinado elemento con el conjunto difuso.
La forma de la función característica utilizada dependerá del criterio aplicado en la resolución de cada problema y variará en función de la cultura, geografía, época o punto de vista del usuario. La única condición que debe cumplir una función característica es que tome valores entre 0 y 1 de forma continua.
Las funciones características más comúnmente utilizadas por su simplicidad matemática y su manejabilidad son la triangular (a), la trapezoidal (b), la gaussiana (c) y la sigmoidal (d). En la siguiente figura se puede ver la forma de estas funciones:
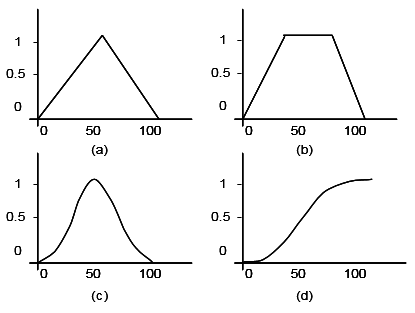
Como podemos ver, la principal dificultad que nos encontraremos al utilizar modelos basados en lógica difusa es la selección de esta función, ya que de ella dependerá el matiz que demos a los objetos que clasifiquemos y, por ende, el éxito de nuestro modelo.
Dicho esto, ¿cómo nos puede ayudar la lógica difusa en el trading? Básicamente tenemos dos campos de aplicación:
- Por un lado, podemos diseñar herramientas que nos permitan medir el grado de veracidad de las señales proporcionadas por un indicador u oscilador. ¿Cómo de fiable es un cruce de medias? ¿En qué condiciones es más o menos válida una señal generada por un RSI? ¿Qué consideramos una variación importante en relación a la rotura de un rango?
- Por otro lado, podemos tratar de buscar estrategias altamente robustas, no centrándonos tanto en optimizar su rentabilidad sino en optimizar la veracidad de dicha rentabilidad.
En próximos artículos, seguiremos profundizando en la aplicación del concepto de lógica difusa a las estrategias de trading con algunos ejemplos prácticos.
Saludos,
X-Trader








