Retomamos la serie sobre técnicas de Machine Learning aplicadas al trading. En esta entrega veremos cómo modelizar relaciones entre variables usando la regresión con Splines.
¿Qué son Splines?
Según nos explica la Wikipedia, un Spline es “una curva diferenciable definida en porciones mediante polinomios”. Se trata de una técnica matemática que combina y extiende las características de la regresión polinómica y las funciones de tipo stepwise. Con los Splines podemos resolver problemas de interpolación, corrigiendo el comportamiento errático de una tendencia usando ajustes de funciones polinómicas troceadas, cuyos puntos de conexión se denominan nodos o knots.
Por supuesto, esas funciones polinómicas no pueden ser de cualquier tipo, exigiéndose que tanto las funciones como sus derivadas primera y segunda sean continuas en los nodos definidos.
Matemáticamente, un Spline S(x) se define como:
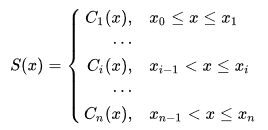
El grado de los polinomios define el grado del spline, de tal forma que si, por ejemplo, alguna de las funciones Ci(x) es cúbica, diremos que tenemos un spline cúbico.
A la hora de estimar splines deberemos determinar básicamente tres aspectos:
- El tipo de interpolación, para lo cual contamos con múltiples variantes de splines como Hermite, Catmull-Rom, Cúbica Natural, B-Splines, NURBS, etc.
- El grado máximo de la función polinómica que usaremos para suavizar la curva.
- El número de nodos o knots.
Posiblemente esta primera explicación así a lo bruto les haya dejado un poco asustados, así que vamos a ver de forma más gráfica esto de los Splines. Imaginemos que nos dan esta nube de puntos y ajustamos un modelo mediante una recta de regresión:
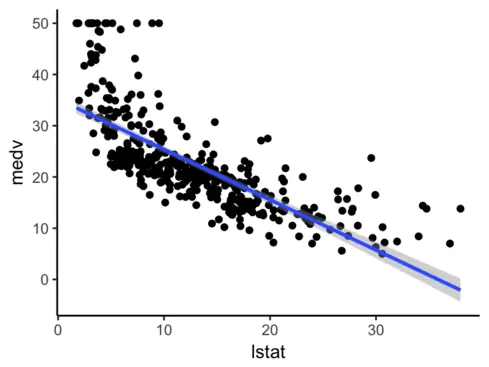
No está mal, pero seguramente una regresión polinomial quedará bastante mejor:
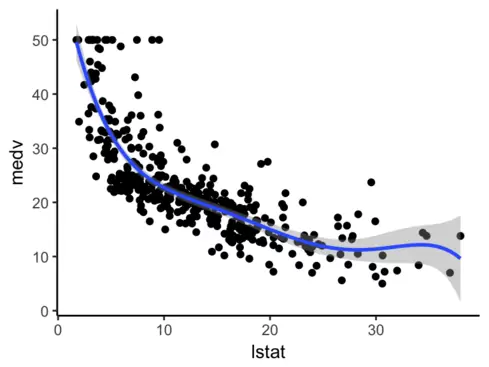
Aunque sin lugar a dudas el mejor ajuste lo lograremos con Splines, porque nos van a permitir amoldarnos mejor usando diferentes funciones combinadas. En este ejemplo en particular, hemos utilizado un spline cúbico con 3 nodos:
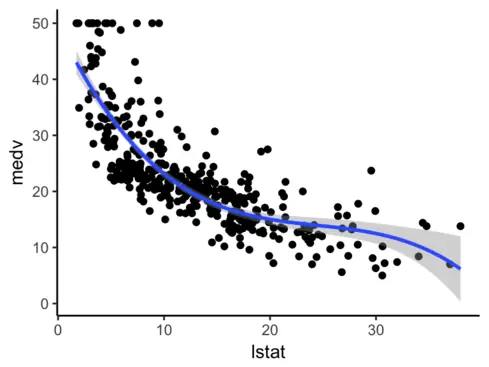
Ahora que más o menos tienen una idea de cómo funcionan y del potencial que tienen, ¡pasemos a la acción!
Modelizando con Splines
Bien, veamos cómo modelizar una relación entre dos variables usando splines. Para ello, vamos a analizar la relación entre el comportamiento del S&P500 y el VIX. En particular, vamos a tratar de predecir si el VIX de la sesión anterior nos permite predecir el valor del S&P 500 de la siguiente sesión. Para ello cargamos las librerías Quantmod y Dplyr y cargamos datos:
library(quantmod)library(dplyr)getSymbols(c("^GSPC","^VIX"))
Para no hacernos trampas al solitario, retardamos un valor el VIX y quitamos el primer valor del S&P500:
SPData <- data.frame(GSPC$GSPC.Close[2:3064])
VIXData <-data.frame(VIX$VIX.Close[1:3063])
Hagamos un plot rápido con regresión lineal incorporada para ver qué pinta tiene la relación entre el VIX de ayer y el S&P500 de mañana:
df<-data.frame(SPData,VIXData)
library(ggplot2)
ggplot(df, aes(x=VIX.Close, y=GSPC.Close)) + geom_point(shape=1) + geom_smooth(method=lm , color="red", se=FALSE)
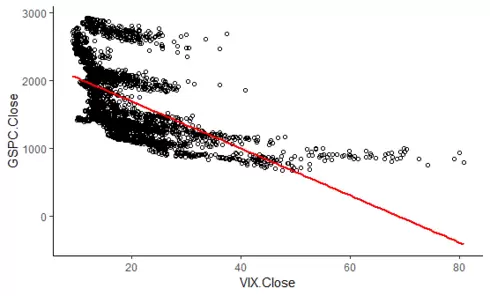
Vaya, parece que utilizar una relación lineal para modelizar estas variables no es lo más adecuado, ¿verdad? Veamos qué tal va la cosa con un spline cúbico. Para ello, en primer lugar creamos nuestros conjuntos de entrenamiento y de prueba (observad que hemos etiquetado las columnas igual, esto nos permitirá ahorrarnos problemas después con las funciones lm y predict):
datatrain<-data.frame(VIXData[1:3000,],SPData[1:3000,])
names(datatrain) <- c("VIX", "SP")
datatest<-data.frame(SPData[3001:3063,],VIXData[3001:3063,])
names(datatest) <- c("VIX", "SP")
Ahora que temenos todos los datos, vamos a ajustar un spline cúbico a nuestros datos. Para ello necesitamos la librería Splines de R:
library(splines)
Previamente debemos seleccionar el número de nodos. Para este ejemplo vamos a seleccionar 3 utilizando los cuartiles de la distribución, tal que:
knots <- quantile(datatrain$VIX, p = c(0.25, 0.5, 0.75))
Ahora tan solo basta con estimar el modelo especificando el spline:
model <- lm (SP ~ bs(VIX, knots = knots, degree=3), data=datatrain)
En la ecuación anterior, con Knots especificamos los nodos que hemos calculado previamente mientras que degree denota el grado máximo de los polinomios que componen el spline.
El resultado de la estimación es el siguiente:
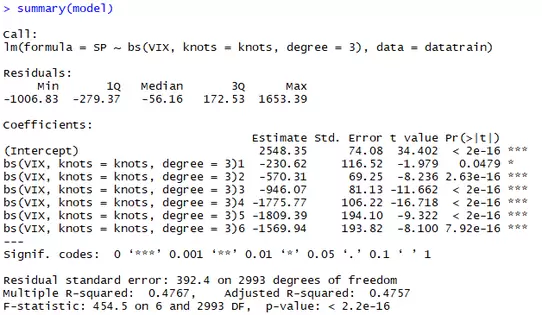
Como podemos ver, todos los coeficientes obtenidos son significativos (el valor absoluto de todos los estadísticos t es superior a 1.96). Eso sí, debemos tener en cuenta que los coeficientes de un spline no son interpretables, esto es, no podemos darles un significado.
Gráficamente el ajuste tiene este aspecto:
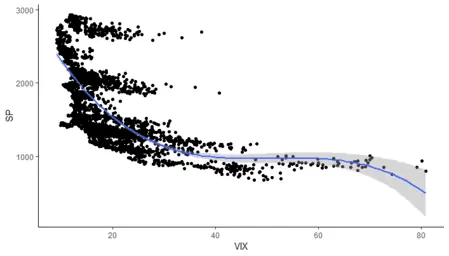
Hagamos algo de predicción con el modelo obtenido. Para ello simplemente debemos usar la función predict y tener cuidado de que los nombres de las variables sean iguales que los de las columnas en los dataframes:
predictions <- model %>% predict(datatest)
Obtenemos los errores cuadráticos medios de las predicciones obtenidas así como el nivel de ajuste:
data.frame(RMSE = RMSE(predictions, datatest$SP), R2 = R2(predictions, datatest$SP))

El resultado tiene bastante buena pinta, veamos gráficamente qué aspecto tiene el asunto:
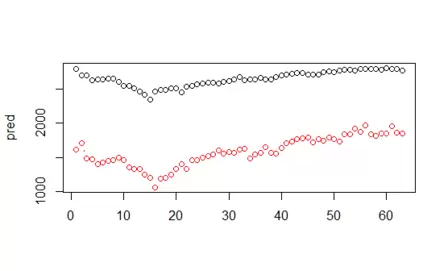
Como podemos ver en el gráfico anterior, si bien los valores de las predicciones (rojo) están sistemáticamente por debajo de los verdaderos valores del S&P 500 (negro) lo cierto es que parece acertar bastante bien la dirección.
Conclusión
Hemos realizado un interesante ejercicio de predicción con Splines que nos ha dado un resultado bastante bueno (ya tocaba, ¿no? :D) a pesar de que a priori no cabía esperar un gran valor predictivo del VIX sobre el S&P500. Por supuesto a partir del código que hemos visto en el artículo basta con que cambien las series a modelizar, y utilicen diferentes tipos de splines variando los nodos y el grado de los polinomios para crear nuevos modelos.
Eso sí, tampoco piensen que los Splines son la panacea: a la hora de usar esta técnica deben tener en cuenta que son funciones que presentan mucha varianza en los extremos superior e inferior del predictor, lo que genera intervalos de confianza muy amplios. Esto es así debido a que la primera y última región carecen de restricción de continuidad en uno de sus extremos, por lo que presentan un exceso de flexibilidad. Este problema se resuelve con una variante de los Splines, los Natural Splines, ya que incorporan una restricción extra, exigiendo que la función sea lineal en los extremos.
Por supuesto, si realizan experimentos con splines, estaré encantado de que compartan sus resultados en el Foro.
Saludos,
X-Trader





