Hace unos meses la gente de Darwinex publicó en su blog un excelente análisis sobre el Darwin DWC, sobre el cual me he inspirado para escribir este artículo. El objetivo de dicho análisis es confirmar si la serie de DWC presenta un comportamiento de reversión a la media o no. Para ello se utilizan diferentes tests estadísticos:
- Exponente de Hurst
- Test de Dickey-Fuller Aumentado (ADF)
- Vida media
Pero antes de ponernos a hacer números, veamos en qué consiste exactamente el Darwin DWC.
El Darwin DWC
El objetivo del Darwin DWC es el de medir en tiempo real como están posicionados los traders que participan en el ecosistema de Darwinex.
Algunas características de este Darwin son:
- Liquidez accesible en todo momento durante los 5 días de la semana.
- Nos permite comprar el sentimiento de mercado sin necesidad de recurrir a otros productos externos tales como ETFs.
- Presenta un comportamiento cíclico, tendiendo a revertir a la media tal y como podemos ver en el siguiente gráfico:
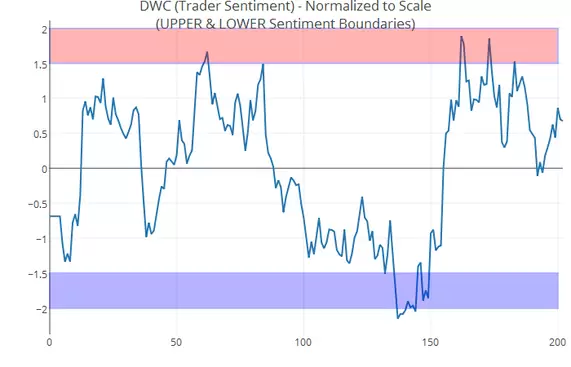
- Es altamente invertible, pudiendo llegar sin problema a una inversión entre 1.200 y 1.500 millones de dólares.
- Este Darwin presenta un comportamiento opuesto al del colectivo de Darwins que hay en Darwinex. Por este motivo su valor sube cuando los traders presentan una marcada aversión a las pérdidas (aguantan posiciones perdedoras mientras que cierran posiciones ganadoras demasiado pronto). En particular, en la escala de atributos de este Darwin, el atributo La (Loss Aversion) se mueve en torno a 9.
Por estos motivos, los inversores que compran Darwins generalmente usan DWC para:
- Cubrirse durante movimientos de mercado violentos que afecten al valor de los Darwins.
- Aprovechar su comportamiento cíclico estable para operarlo y generar ganancias.
Ahora que ya sabemos en qué consiste este Darwin, veamos un análisis cuantitativo de su comportamiento para ver si, en efecto, lo que nos sugiere su gráfico visualmente podemos corroborarlo mediante diferentes tests estadísticos.
En Busca de la Reversión a la Media
Veamos en qué medida se verifica nuestra hipótesis de que DWC revierte a la media. Para ello usaremos los rendimientos de este Darwin con una resolución de 1 minuto.
1. Exponente de Hurst
La propiedad de reversión a la media de una serie temporal puede ser evaluada en términos de su tasa de difusión desde su origen. En particular, una serie X que presenta reversión a la media se verificará que:
Tasa de Difusión (X) < Tasa de Difusión de un Paseo Aleatorio Geométrico
La tasa de difusión se puede medir como la varianza del logaritmo de la serie temporal, tomando un intervalo temporal aleatorio T:
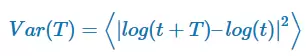
Si la serie temporal se comporta como un Paseo Aleatorio Geométrico, entonces se cumple que Var(T) ~ T a medida que se incrementa T:
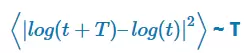
Si por el contrario la serie temporal presenta un comportamiento tendencial o revierte a la media, entonces se verificará que:
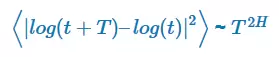
Donde H es lo que se conoce como Exponente de Hurst, una medida de hasta qué punto una serie es persistente (presenta una tendencia) o antipersistente (presenta reversión a la media). En particular:
- Si H > 0.5, la serie es tendencial.
- Si H = 0.5, la serie se comporta como un paseo aleatorio geométrico.
- Si H < 0.5, la serie presenta reversión a la media.
Podemos calcular el exponente de Hurst para DWC usando la librería pracma de R:
library(pracma)
# Print M1 data Hurst Exponent
> hurstexp(log(DWC.M1$quote))
Simple R/S Hurst estimation: 0.8962816
Corrected R over S Hurst exponent: 0.9945418
Empirical Hurst exponent: 1.001317
Corrected empirical Hurst exponent: 0.9938308
Theoretical Hurst exponent: 0.520278
Dado que el exponent de Hurst obtenido (0.520278) es ligeramente superior a 0.5 no podemos asegurar que exista reversión a la media, comportándose de manera similar a la de un paseo aleatorio.
2. Test de Dickey-Fuller Aumentado (ADF)
Si la serie temporal de DWC no se comportase como un paseo aleatorio, entonces cualquier valor de la misma tendría una relación proporcional con el siguiente valor de la serie.
Si la serie revierte a la media, entonces cualquier movimiento por encima de su media seguramente sea seguido de un movimiento por debajo y viceversa.
El test ADF analiza la presencia de raíces unitarias en las series temporales que presenten naturaleza autorregresiva, y la tendencia a revertir a la media de una serie temporal.
Consideremos el siguiente modelo autorregresivo de orden p:
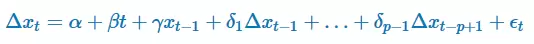
El test ADF evalúa estadísticamente si se acepta o rechaza la hipótesis nula γ = 0.
Si la hipótesis se rechaza, entonces la serie temporal no será un paseo aleatorio, existiendo una relación lineal entre valores consecutivos de la serie DWC.
El test ADF puede realizarse fácilmente con R usando la librería urca:
> library(urca)
> summary(ur.df(DWC.M1$quote, type="drift", lags=1))
###############################################
# Augmented Dickey-Fuller Test Unit Root Test #
###############################################
Test regression drift
Call:
lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)
Residuals:
Min 1Q Median 3Q Max
-1.66860 -0.01990 0.00008 0.02011 1.16945
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0347880 0.0114228 3.045 0.00232 **
z.lag.1 -0.0003287 0.0001075 -3.057 0.00224 **
z.diff.lag -0.0365180 0.0045255 -8.069 7.22e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.04493 on 48479 degrees of freedom
Multiple R-squared: 0.001542, Adjusted R-squared: 0.001501
F-statistic: 37.45 on 2 and 48479 DF, p-value: < 2.2e-16
Value of test-statistic is: -3.0566 4.849
Critical values for test statistics:
1pct 5pct 10pct
tau2 -3.43 -2.86 -2.57
phi1 6.43 4.59 3.78
Analicemos los resultados obtenidos:
z.lag.1 hace referencia al parámetro asociado al retardo de la variable X, esto es, γ. Por su parte, tau2 son los valores críticos para realizar el test sobre la hipótesis nula (γ=0).
Para rechazar la hipótesis nula el valor del estadístico t obtenido debe ser menor que el valor crítico tau2 (al 1%, 5% y 10% de significación).
Dado que z.lag.1 = -3.0566 es menor que los valores críticos al 5% y 10% podemos rechazar la hipótesis nula por lo que la probabilidad de que DWC presente un comportamiento estacionario es muy alta.
Repitiendo este test en otros timeframes (30 minutos, 1 hora, 2 horas, 4 horas, diario) se obtuvieron resultados similares, rechazando la hipótesis nula en todos los casos.
3. Vida media de un proceso de reversión a la media
Una alternativa al modelo autorregresivo lineal que hemos visto en el apartado anterior sería analizar cuánto tiempo tarda la serie en revertir a su media.
Por definición, las variaciones en el próximo valor periódico de una serie temporal que revierte a la media son proporcionales a la diferencia entre la media histórica de la serie y su valor actual. Cuando se verifica esta condición se dice que la serie es un proceso de Ornstein-Uhlenbeck.
La diferencia anterior nos permite expresa el valor esperado de una serie x(t) tal que:
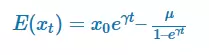
Si DWC es una serie que revierte a la media, y el valor de γ es negativo, entonces la ecuación anterior nos dirá que DWC decae exponencialmente, con una vida media de -log(2)/γ.
Por tanto, deberemos estimar el valor de γ y ver si es negativo. Si ello fuera así, calcularemos su vida media y valoraremos si es una duración aceptable para plantear una estrategia de reversión a la media en DWC. Para ello nuevamente recurriremos a la utilización de código en R.
Paso 1: calculamos γ y comprobamos su signo.
> M1.data <- as.ts(DWC.M1$quote)
> M1.data.lag <- lag(M1.data, -1)
> M1.data.delta <- diff(M1.data)
> M1.data.frame <- cbind(M1.data, M1.data.lag, M1.data.delta)
> M1.data.frame <- M1.data.frame[-1,]
> M1.regression <- lm(M1.data.delta ~ M1.data.lag, data=as.data.frame(M1.data.frame))
> gamma <- summary(M1.regression)$coefficients[2]
> print(gamma)
[1] -0.0003588994
El valor obtenido para γ es negativo (-0.0003588994), por lo que podemos considerar que DWC en el marco temporal de 1 minuto revierte a la media.
Paso 2: calculamos la vida media y valoramos si nos puede resultar útil para plantear una estrategia.
> M1.data.half.life <- -log(2) / gamma
> print(paste("Half-life: ", M1.data.half.life, " minutes, or ", M1.data.half.life/60, " Hours", sep=""))
[1] "Half-life: 1931.31306610404 minutes, or 32.1885511017341 Hours"
La vida media estimada para DWC es de 1.931 minutos. Una forma de aprovechar este dato es dibujar una media móvil de ese período. Si graficamos esa media sobre la serie obtenemos el siguiente gráfico:
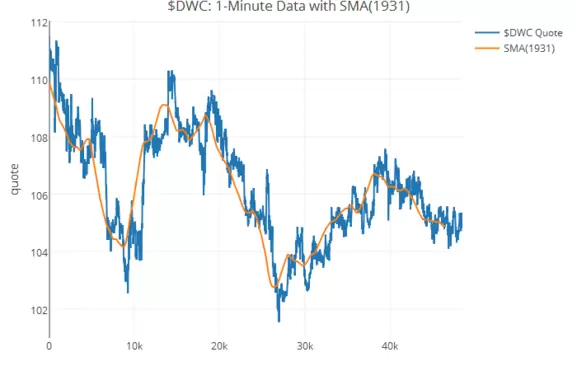
Como podemos observar en el gráfico anterior, el precio de DWC tiene a revertir de forma bastante regular a la media calculada.
Conclusión
Tras realizar tres tests estadísticos para evaluar si la serie de DWC en gráfico de 1 minuto presenta cierto grado de reversión a la media, los resultados obtenidos han sido los siguientes:
- El exponente de Hurst no ha confirmado la existencia de reversión a la media, siendo el comportamiento más similar al de un paseo aleatorio.
- El test Dickey-Fuller aumentado muestra que la serie DWC es estacionaria al 95% de confianza.
- El test de Vida Media sí ha confirmado que existe un comportamiento de reversión a la media.
Ahora que ya sabéis cómo realizar diferentes tests estadísticos para analizar si una serie presenta reversión a la media podéis realizar vuestros propios análisis con las series que deseéis. En particular, si queréis reproducir este ejercicio con los datos actualizados para el Darwin DWC podéis bajaros toda la serie desde el GitHub de DarwinexLabs.
Por último, como complemento a este artículo os recomiendo que echéis un vistazo a este análisis de DWC que ha realizado Tiotino en su excelente blog Trading y Python.
Saludos,
X-Trader