Poemas e Imágenes Preliminares
La forma más fácil de empezar a explicar cómo es un elefante es mostrar primero a alguien una foto. Vd. señala y dice: «Mira. Un elefante». Así que aquí hay una foto de un fractal, algo que se llama una alfombra de Sierpinski:
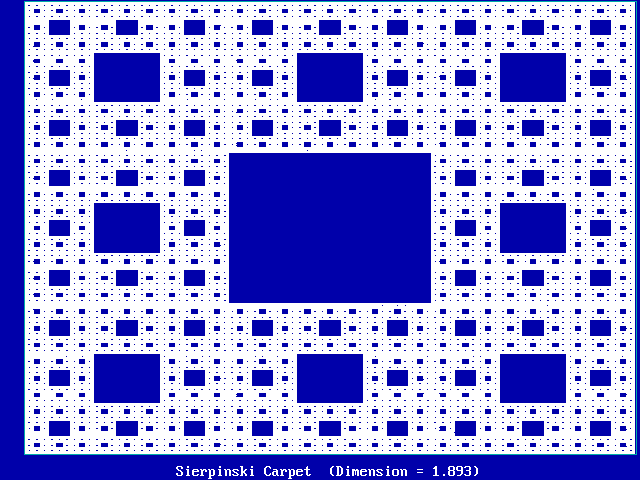
Observe que tiene un cuadrado azul en el centro, con 8 cuadrados más pequeños adicionales alrededor del cuadrado central.

Cada uno de los 8 cuadros pequeños se parece al cuadrado original. Multiplicando cada lado de un cuadrado más pequeño por 3 (aumentando el área de 3 x 3 = 9), se obtiene el cuadrado original. O bien, haciendo lo contrario, dividiendo cada lado del cuadrado original grande por 3, obtenemos uno de los 8 cuadrados más pequeños. Con un factor de escala de 3, todos los cuadrados tienen el mismo aspecto (dejando a un lado el cuadrado del centro).
Por tanto, podemos obtener 8 copias del cuadrado original con un factor de escala de 3. Más adelante veremos que esto define una dimensión fractal igual a log 8 / log 3 = 1.8927. (Aunque lo veremos más adelante, observe que la dimensión no es un bonito número entero como 2 o 3.)
Cada uno de los cuadrados más pequeños también se puede dividir de la misma manera: un cuadrado azul central rodeado por 8 cuadrados aún más pequeños. Así que los 8 cuadrados pequeños originales pueden ser divididos en un total de 64 cuadrados cada uno –cada uno de los cuales tendrá el mismo aspecto que el cuadrado original si multiplicamos sus lados por 9. Por lo tanto la dimensión fractal es log 64 / log 9 = 1,8927. (No esperaría que la dimensión cambiara, ¿verdad?) En un fractal, este proceso continúa para siempre.
Mientras tanto, sin darnos cuenta, acabamos de definir lo que es una dimensión fractal (o dimensión de Hausdorff). Si el número de cuadrados pequeños cuadrados es N con un factor de escala r, entonces estos dos números están relacionadas por la dimensión fractal D tal que:
N = rD
O, despejando D y tomando logaritmos, tendemos que D = log N / log r.
Veamos ahora un poema sobre pulgas fractales:
Hobbes clearly proves that every creature
Lives in a state of war by nature;
So naturalists observe a flea
Has smaller fleas that on him prey,
And these have smaller still to bite ’em,
And so proceed ad infinitum.
Swift, J. (1733), Poetry: a Rhapsody
Bien, esto en cuanto a un análisis preliminar de los fractales. Vamos a echar un vistazo preliminar al Caos, preguntándonos qué es un sistema dinámico.
Sistemas Dinámicos
¿Qué es un sistema dinámico? He aquí uno: Juanito crece 5 centimetros por año. Este sistema explica cómo la altura de Johnny cambia con el tiempo. Sea x(n) la altura de Johnny este año. Mientras que su altura el año será x(n + 1). Entonces podemos escribir el sistema dinámico en la forma de una ecuación como:
x(n + 1) = x(n) + 5
¿Lo ve? ¿No son simples las matemáticas? Si introducimos la altura actual de Johnny de x(n) = 96 cm. en el lado derecho de la ecuación, obtenemos la altura de Johnny para el próximo año:
x (n + 1) = x (n) + 5 = 96 + 5 = 101 cm
Pasar del lado derecho de la ecuación al izquierdo es lo que se denomina una iteración. Podemos iterar de nuevo introduciendo la nueva altura de 101 cm de Johnny en el lado derecho de la ecuación (es decir, x(n) = 101), y obtener x(n + 1) = 101+5 = 106. Si iteramos la ecuación una tercera vez, obtenemos la altura de Johnny en 3 años, es decir, 111 cm, a partir de una altura de 96 cm).
Este es un sistema dinámico determinista. Si quisiéramos que sea no determinista (estocástico), podríamos dejar que el modelo sea: Johnny crece 5 cm al año, más o menos, y escribir la ecuación como:
x(n + 1) = x(n) + 5 + u
donde u es un pequeño término de error (pequeño en relación a 5), y sigue una determinada distribución de probabilidad.
Volvamos a la ecuación determinista original. La ecuación original, x(n + 1) = x(n) + 5, es lineal. Lineal significa que o bien sumamos variables o constantes, o multiplicamos variables por constantes. Así, la ecuación z(n + 1) = z(n) + 5y(n) – 2x(n) es lineal, por ejemplo. Pero si se multiplican variables juntas, o elevamos alguna de ellas a una potencia diferente de 1, la ecuación (sistema) es no lineal. Por ejemplo, la ecuación x(n + 1) = x(n)2 es no lineal debido a que x(n) se eleva al cuadrado. La ecuación z = xy también es no lineal debido a que dos variables, X e Y, se multiplican entre sí.
Bueno. Basta de esto. ¿Qué es el Caos? Aquí tiene una imagen de caos. Las líneas muestran cómo un sistema dinámico (en particular, un sistema de Lorenz) cambia con el tiempo en un espacio tridimensional. Observe cómo la línea (ruta, trayectoria) dibuja bucles infinitos, que nunca se cortan entre sí.

Observe también que el sistema mantiene un bucle en torno a dos áreas generales, como si fuera atraído por ellas. Los puntos a los que un sistema se siente obligado a ir en una dirección determinada se denominan cuenca de atracción. El lugar al que va se llama atractor.
Aquí tenemos una ecuación cuyo atractor es un único punto, el cero:
x(n + 1) = 0.9 x(n)
No importa en qué valor comience x(n), el siguiente valor, x(n + 1), es sólo el 90 por ciento de eso. Si se mantiene la iteración de la ecuación, el valor de x(n + 1) se aproxima a cero.
Algunos atractores son simples círculos o bucles cerrados –como si fuera un trozo de cuerda irregular con los extremos conectados. Estos son los llamados ciclos límite.
Otros atractores, como el atractor de Lorenz anterior, son más raros. Por ello se denominan atractores extraños.
Bien, ahora vamos a definir el caos.






