Mucho revuelo se ha montado en el Foro en torno al sistema de apuestas Labouchere Inverso que aparece en el libro de Norman Leigh, 13 Contra la Banca. Ello me motivó a investigar de un modo científico si realmente este sistema aplicado a sucesos con diferentes probabilidades tenía posibilidades de éxito y presentarlo en la última kedada. Y los resultados, que coinciden con los de otros foreros, no son todo lo buenos que esperábamos después de leer el libro.
El objetivo es contestar a la pregunta de si el sistema Labouchere Inverso es rentable en muestras relativamente grandes (o lo que es lo mismo, a largo plazo, considerando un número grande de tiradas de ruleta o de operaciones de un sistema, decidí utilizar Simulaciones de Monte Carlo, muy apropiadas dado que se trata de analizar un juego ;-). Utilizando Matlab programé el siguiente script, que permite simular miles e incluso millones de tiradas variando la serie de partida (arr), la apuesta máxima que admite la mesa (maxbet) y la ventaja o desventaja de la banca frente al jugador (prob). La variable spins por su parte controla que el programa no se desmadre más allá de 10.000 tiradas para evitar problemas aunque en ningún momento fue necesario parar la ejecución:
arr = [1:1:4];
arr2=arr;
maxbet = 1000;
prob=0.5;
spins=10000;
win = [];
loss = [];
profit = [];
rset=0;
for i=1:spins
while(arr(1)+arr(end)<maxbet)
outcome = rand;
if outcome > prob
apuesta = arr(1) + arr(end);
win = horzcat(win,apuesta);
arr = horzcat(arr, apuesta);
loss = horzcat(loss,0);
else
apuesta = arr(1) + arr(end);
loss = horzcat(loss,apuesta);
arr = arr(2:end-1);
win = horzcat(win,0);
end
if isempty(arr)
arr=arr2;
rset=rset+1;
end
resta = sum(win)-sum(loss);
profit=horzcat(profit, resta);
i=i+1
end
end
Con este script sólo se simula un primer «hongo» como los que aparecen en el libro. Una vez simulado el primero se pueden generar millones de experimentos ejecutando el bucle varias veces.
A continuación se presentan los resultados del beneficio o pérdida obtenido a largo plazo (100.000 tiradas) variando diferentes variables.
PRUEBA 1: ¿CÓMO AFECTA UNA VARIACIÓN DE LA SERIE DE PARTIDA INICIAL?
Las series utilizadas son:
1, 2, 3, 4
1, 2, 3, …, 10
1, 2, 3, …, 10, 11, 12, …, 20
La apuesta máxima es de 1.000 uds. en todos los casos y se supone que no existe ventaja para ningún jugador (prob = 0.50). Los gráficos de resultados se presentan a continuación; en ellos, Resets hace referencia al número de veces que se alcanza un hongo a lo largo de la simulación (reseteando la serie), Min y Máx son respectivamente la pérdida y el beneficio máximo alcanzados, Avg es la media de los beneficios y RR es el ratio Máx/Mín para ver cuánto llegamos a arriesgar durante la simulación vs. el beneficio máximo que podríamos obtener.
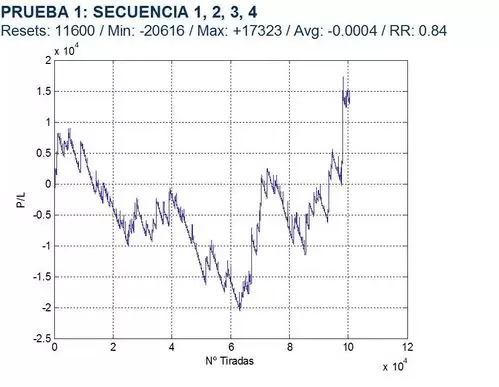
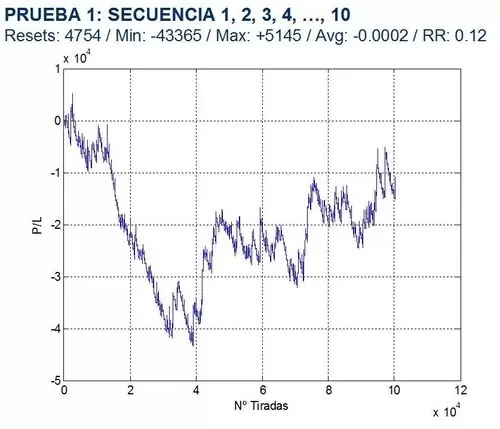
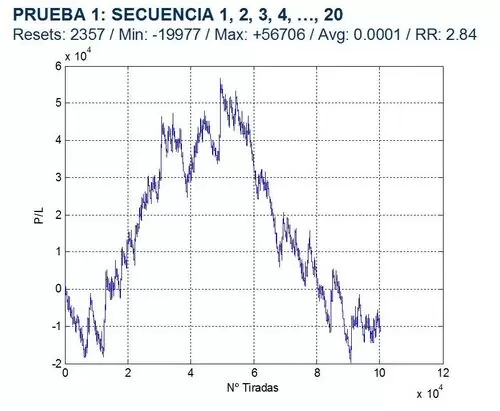
Los resultados no parecen ser concluyentes, observándose una cierta disparidad de comportamientos.
PRUEBA 2: ¿CÓMO AFECTA UNA VARIACIÓN DE LA VENTAJA DEL JUGADOR FRENTE A LA BANCA?
Simulamos resultados para una ruleta que da mayor ventaja a la banca (prob>0.75), sin ventaja para ninguna de las partes (prob>0.50) y con ventaja para el jugador (prob.>0.25). La serie utilizada es 1, 2, 3, 4 y la apuesta máxima es de 1000 uds. en todos los casos. Los resultados obtenidos se muestran a continuación:
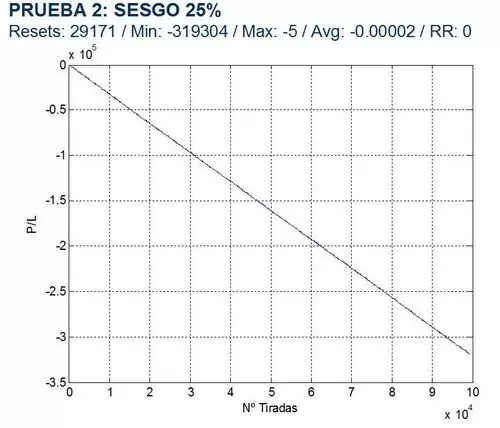
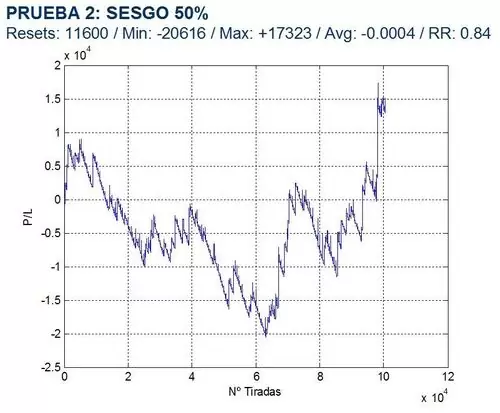
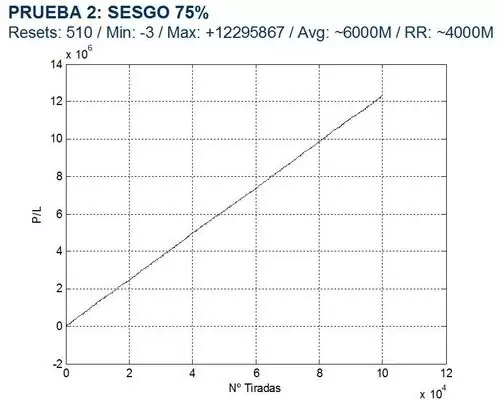
En este caso, la conclusión es evidente: si jugamos con ventaja frente a la banca, los beneficios se disparan de forma explosiva mientras que si la banca es la que tiene ventaja, las pérdidas aumentan pero mucho más despacio que los beneficios en el caso contrario.
PRUEBA 3: ¿CÓMO AFECTA UNA VARIACIÓN DE LA APUESTA MÁXIMA PERMITIDA?
Comprobemos ahora el impacto de una variación de la apuesta máxima permitida por la mesa. Para ello consideré los siguientes valores para maxbet: 100, 1.000 y 100.000, suponiendo en todos los casos, prob=0.5 y arr=1, 2, 3, 4. Debajo tienen los resultados obtenidos:
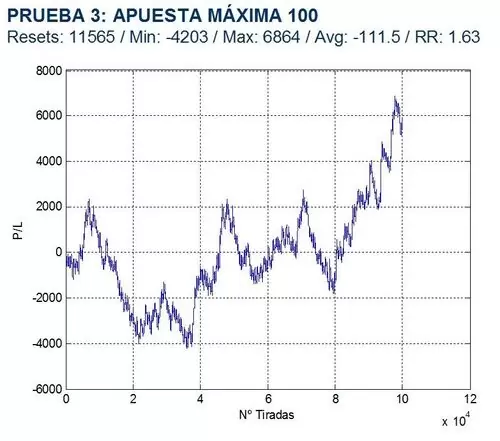
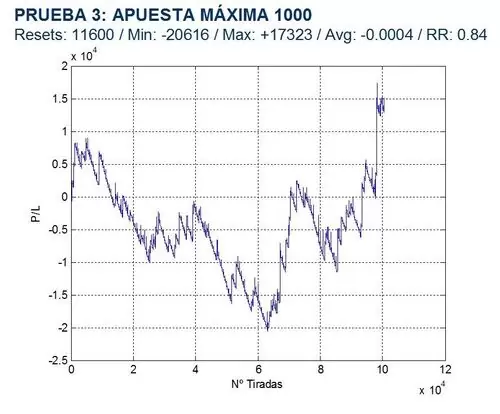
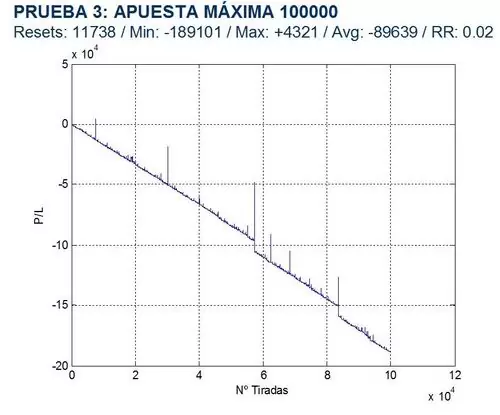
Como pueden observar, cuanto mayor es la apuesta máxima permitida, más tiempo estaremos jugando y por tanto más probable será que al final perdamos el capital ganado. Por el contrario, asegurar ganancias pequeñas rápidamente (maxbet=100) parece ser una opción rentable.
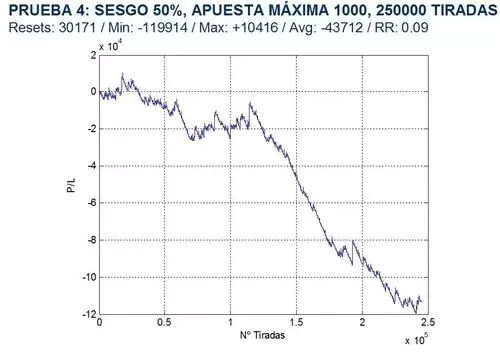
PRUEBA 4: LABOUCHERE INVERSO A LARGO PLAZO
Finalmente decidí realizar una última simulación aumentando el número de tiradas bajo estos supuestos: maxbet=1.000, prob=0.5, arr=1, 2, 3, 4, para ver a que convergía la serie más allá de las 100.000 tiradas, concretamente 250.000. El resultado es que a muy largo plazo este sistema de apuestas es perdedor.
CONCLUSIONES
- El impacto de la secuencia que elijamos no parece tener un impacto significativo a largo plazo, si acaso puede tener un cierto impacto al comienzo del juego.
- Una posible ventaja del jugador frente a la banca permite multiplicar exponencialmente los beneficios con este sistema, mientras que en el caso opuesto, las pérdidas parece crecer más despacio.
- La apuesta máxima a partir de la cual reseteamos la serie afecta significativamente a los resultados, hasta el punto de que, si nunca reseteamos la serie, perderemos a largo plazo, incluso en el caso de que no exista ventaja para ninguno de los jugadores.
- El sistema Labouchere Inverso permite mejorar el comportamiento de cualquier sistema con una fiabilidad superior al 50%… al igual que lo haría cualquier antimartingala.
- Suponiendo que la historia de Norman Leigh fuera cierta, sólo pudo lograrlo con suerte o detectando algún sesgo en alguna de las ruletas que pudiera dar ventaja al jugador a largo plazo.
X-Trader






