Aquí tenéis otra posible estrategia de Money Management (MM) totalmente distinta a las que aparecen en libros de Van Tharp, Ralph Vince, etc. La encontré por un foro americano de Money Management, así que disculpad si encontráis algunos errores de redacción pues se trata de una traducción y compilación de varios post, con sus respuestas, integrando posteriormente todo esto en un texto compacto lo que resulta algo complicado. Es probable que muchos la conozcáis, e incluso que no os guste, pero seguro que todos la consideráis distinta al típico Fixed Fractional Method (FFM) que muchos utilizamos. Espero que os parezca interesante y que nos ayude a abrir la mente para que cada uno pueda ir pensando estrategias propias y, sobre todo, distintas a las que utiliza la mayoría.
THE STOP TRADING METHOD
Antes de comenzar debe quedar claro que Money Management (MM) no es lo mismo que Position Management (PM). El número de contratos que decides abrir en una determinada operación es MM. El lugar donde colocas el stop para una determinada operación es PM. Un uso correcto del MM permite que una estrategia de trading ganadora genere unos beneficios geométricamente superiores, mientras que se mantenga relativamente bajo el riesgo de ruina. Sin embargo, una estrategia perdedora no podrá ser transformada en ganadora a través de ninguna estrategia de MM. Así que nuestro primer paso será desarrollar un sistema de especulación ganador.
Una vez tengamos desarrollado nuestro sistema ganador, deberemos saber un par de cosas sobre sus características. Necesitaremos saber su máximo Drawdown (en adelante max. DD) y el % de operaciones perdedoras antes de poder aplicarle una buena estrategia de MM. Es importante, también, tener un histórico de por lo menos 100 operaciones (ya sean reales o sobre el papel) como base de nuestros cálculos. Una vez tengamos todo esto, empecemos con la explicación de esta estrategia de MM.
Lo primero que debemos calcular es con cuánta frecuencia deberíamos obtener un nuevo máximo en el valor de nuestra cuenta. Para ello, utilizaremos el % de operaciones perdedoras. Así es cómo lo haremos: multiplicaremos el % de pérdidas por sí mismo hasta que tengamos un número aproximado a 0.01. Con un ejemplo veremos mejor qué significa esto.
Supongamos que el % de pérdidas de nuestro sistema ganador es de un 60%. Pues bien, tenemos que multiplicar ese 0.6 por sí mismo, tantas veces como sea necesario para obtener un número aproximado a 0.01.
0.6 x 0.6 x 0.6 x 0.6 x 0.6 x 0.6 x 0.6 x 0.6 = 0.6^8 = 0.0167
Esto significa que este método con un 60% de operaciones perdedoras no tendrá más de 8 operaciones perdedoras seguidas con una probabilidad del 99.9833 %. Dicho de otro modo, durante el 99.9833% del tiempo que estemos utilizando el sistema, éste no tendrá una serie superior a 8 operaciones negativas seguidas.
A continuación multiplicaremos ese número (en nuestro ejemplo es el 8) por 3, con lo cual obtenemos 24. A este número es lo que llamaremos Trading Cycle. Dicho ciclo indica el número máximo de operaciones que deberíamos realizar antes de obtener un nuevo máximo en la cuenta. Coge el histórico de tu sistema y haz marcas en tu performance cada 24 operaciones y fíjate si se cumple este principio. Si no se cumple, probablemente el % de pérdidas real sea mayor que el que has utilizado para calcular el Trading Cycle. Usa un % mayor hasta que concuerden los máximos de tu cuenta con el Trading Cycle de tu sistema.
El siguiente paso será saber con cuántos contratos podrás empezar a operar en tu cuenta. Esto dependerá de la cantidad de sufrimiento que psicológicamente seas capaz de soportar. Cuanto mayor sea tu capacidad de soportar dolor, mayor número de contratos deberás emplear y a la inversa. Una vez hayas decidido el máximo DD que consideras soportable, multiplica el valor total inicial de tu cartera por ese DD máximo que estás dispuesto a soportar (en porcentaje, claro). Y a continuación divide ese DD máximo aceptable entre el DD máximo que hayas sufrido en tu histórico para obtener el número de contratos con el que empezar a operar.
Por ejemplo, imagina que el tamaño de tu cuenta es de 20.000 € y tu máximo DD aceptable es de un 40%, con lo que 20.000 € x 0,40 = 8.000 €. Si tu histórico muestra un DD máximo de 2.000 €, dividiremos 8.000 € / 2.000 € = 4 contratos. Estos 4 contratos indican el número de contratos con los que deberíamos empezar a operar.
Ya sabemos con cuantos contratos empezar a operar. El siguiente paso será determinar cuándo cambiar el número de contratos. Lo primero de todo, cuando veamos que el máximo DD histórico se ha alcanzado con nuestras operaciones actuales, debemos dejar de operar (seguimos con operativa sobre el papel). Una vez haya terminado este nuevo DD y tengamos un nuevo máximo en el valor de la cartera, utilizaremos este nuevo DD para realizar el cálculo anterior y recalcular nuestros números de MM, empezando, así, otra vez.
Por otro lado, a medida que los beneficios se van incrementando, cogeremos el valor inicial de la cartera (VIC) y lo sumaremos a tres veces (es nuestro filtro) el valor de nuestro peor DD. Una vez que el valor de nuestra cuenta alcance esa cota añadiremos un nuevo contrato con la total tranquilidad de que estamos manteniendo al mínimo nuestro riesgo de ruina. Lógicamente, cuanto más pequeño sea el filtro más agresiva será la estrategia y al contrario.
Supongamos que nuestro VIC es de 20.000 € y nuestro máximo DD es de 2.000 €. Utilizamos la fórmula VIC + (máx. DD x 3) para determinar el valor de nuestra cuenta en el que añadiremos un nuevo contrato.
20.000 € + (2.000 x 3) = 20.000 € + 6.000 € = 26.000 €
Cuando nuestra cuenta alcance el valor de 26.000 € añadiremos un nuevo contrato, pasando de 4 a 5.
Ahora bien, una vez decidamos pasar de 4 a 5 contratos, debemos realizar nuestra operación de MM pero ahora con los nuevos valores para ver si este cambio en el MM es aceptable por nosotros. Es decir, el tamaño de nuestra cuenta ahora será 26.000 € en vez de los 20.000 € anteriores.
Así que multiplicamos dicha cifra por el máximo DD que nuestra psique tolera (en nuestro ejemplo era un 40%) y lo obtenido lo dividiremos entre el peor DD histórico de nuestro sistema (que en el ejemplo eran 2.000 €).
26.000 € x 0,40 = 10.400 €; 10.400 € / 2.000 € = 5,2
Por tanto, el cambio que acabamos de realizar en nuestro MM es perfectamente tolerable y admisible.
Veamos un ejemplo de las curvas producidas por esta estrategia de Money Management en la cartera de su creador, comparándola con la producida por el Fixed Fraccional Method y por el Fixed Contract Method.
En primer lugar tenemos el gráfico original de la curva del equity. Opera con 5 contratos. El beneficio es de 1.41 Millones con un DD máximo de 107.000 €. El máximo DD, en el momento en el que tiene lugar, es de un 16.36%. Por supuesto, esto representa un mayor riesgo potencial puesto que 107.000 € representa un 60% de DD del valor inicial del equity. El Profit Factor es de 2.8.
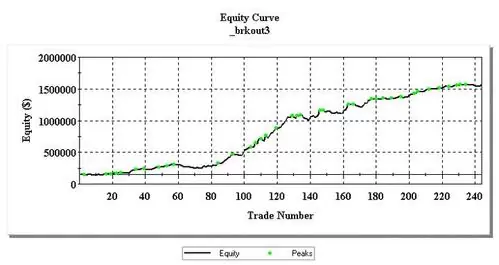
Ahora os muestro la curva del equity utilizando el Fixed Fractional Method fijado en un 5,56% de la cartera arriesgado por operación. El beneficio alcanza los 1.8 Millones con un DD máximo de 391.000 €. El Profit factor ha caído hasta los 2.22. El máximo DD representa un 17.26% en el momento en que tuvo lugar.
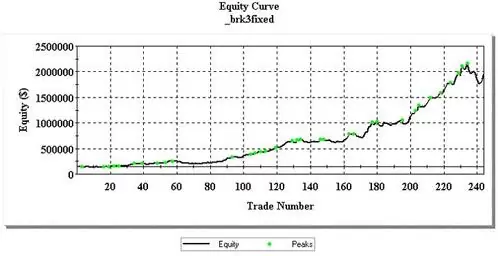
Finalmente os muestro el gráfico de la misma cartera pero utilizando el método de MM anteriormente descrito. El beneficio alcanza los 6.4 Millones con un DD máximo de 729.000 €. El Profit Factor es de 2.48 y el máximo DD representa un 16.34% de la cartera en el momento en el que tuvo lugar.
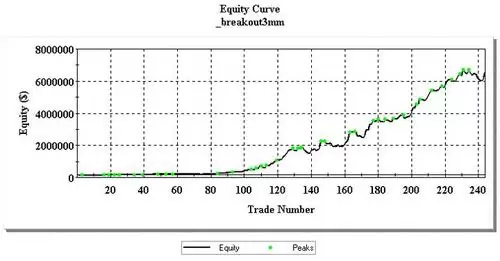
Según el supuesto creador, ha estado utilizando este sistema durante los últimos 14 años, en los cuales ha estado operando profesionalmente. Considera, además, mucho mejor este método que el Fixed Fractional ya que éste último pierde dinero en los juegos de suma cero y su sistema no, ya que en el suyo el número de contratos no se reduce cuando sufrimos un DD mientras que en el FFM sí se reducen.
Para que este modelo funcione correctamente es imprescindible tener un histórico muy detallado y bien estudiado. Es vital que el máximo DD sufrido, que utilizamos para la operación que nos indica el número de contratos con el que operar, sea representativo y fiable, tanto dentro del histórico utilizado para la medición como fuera de él. También, como ya dijimos al principio, es importante que nuestro sistema funcione y tenga una media positiva en un número elevado de operaciones.
Como podéis observar, una de sus principales diferencias (no quiero emplear la palabra ventaja, aunque mucha gente pueda verlo así, pues pretendo ser lo más aséptico posible a la hora de presentar esta estrategia) respecto del Fixed Fractional Method es que esta nueva estrategia de MM no disminuye el número de contratos a medida que estamos inmersos en un DD, sino que una vez alcanzado el peor DD histórico deja de operar. Ahora bien (y siguiendo con la comparación de esta estrategia y el FFM), debemos tener muy en cuenta dos puntos:
1. La estrategia presentada generará mucho más beneficios que los producidos utilizando el FFM si no alcanzamos el peor DD histórico con mucha frecuencia.
2. Sin embargo, si el peor DD es alcanzado con relativa frecuencia, obtendremos peores resultados que con el FFM ya que dejaríamos de operar hasta lograr un nuevo máximo del equity, mientras que con el FFM seguiríamos operando. Además, cuando tenemos un nuevo peor DD, tendremos que recalcular el número de contratos haciendo una reducción de los mismos.
Quinito (Inversor)