Seguramente recuerden un artículo de hace un par de años en el que les explicaba los fundamentos teóricos de la lógica difusa y sus posible aplicaciones en el trading. En este artículo, utilizando la librería FuzzyNet que han publicado recientemente en MQL5.com vamos a ver una aplicación práctica clasificando el comportamiento de un indicador en base a lógica difusa.
Conceptos previos
Si bien ya se introdujo la base conceptual de la lógica difusa en nuestro artículo anterior, vamos a repasar un poco la idea básica con un ejemplo muy sencillo que nos ayudará a repasar la idea básica. Imaginemos dos mundos, el de la lógica clásica y el de la lógica difusa. En el mundo de la lógica clásica, una estrategia automática que opera en el mercado funcionará de la siguiente manera: si se verifica la condición X entonces compro un lote a mercado. Sencillo, ¿verdad? Sin embargo, se trata de un enfoque claramente poco flexible.
Sin embargo, en el mundo de la lógica difusa, la orden de comprar no es tan directa pasando por un filtro similar al que realiza la mente humana cuando decide o no decide ejecutar una operación. Dependiendo de la fortaleza de la señal, podemos operar un lote, medio lote o incluso decidir no operar. Con la lógica difusa, la idea es hacer algo parecido.
Funciones de Pertenencia
Si bien en el artículo anterior vimos de pasada lo que se conoce como funciones de pertenencia o membresía, vamos a verlas en detalle, analizando su formulación matemática.
Función Triangular
Se trata de la función más utilizada en el campo de la lógica difusa, permitiendo representar incertidumbres del tipo “aproximadamente igual”, “valor promedio”, “situado en el rango”, “similar a un objeto”, etc. Su fórmula es la siguiente:
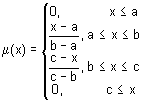
En la ecuación anterior, el rango [a, c] representa el rango de variación de la variable x, siendo b el valor más probable de todos los valores del rango. Visualmente su aspecto es el siguiente:
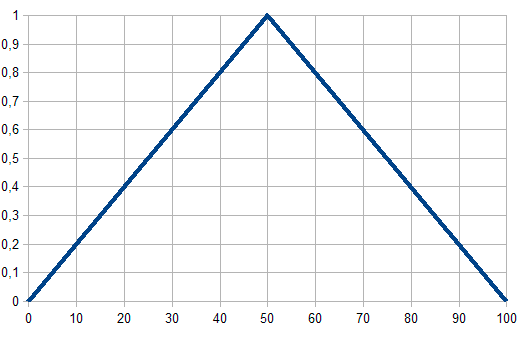
Función Trapezoidal
Esta función viene definida por la siguiente ecuación:
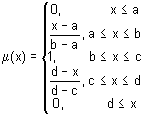
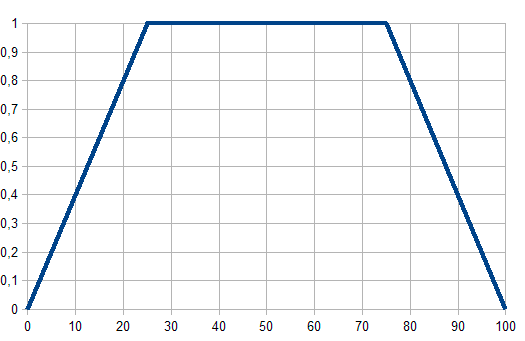
En este caso, la interpretación de la función es la siguiente: el rango [a, d] representa el rango completo de valores de la variable x, mientras que el subconjunto [b, c] representa la valoración más optimista de x.
Visualmente la función tiene este aspecto:
Función Gaussiana
Esta función posee forma acampanada y viene definida por la siguiente ecuación:
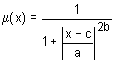
Los valores de los parámetros se interpretan de la siguiente manera: a determina el ratio de concentración (más o menos cerca de la media de la campana); b configura la pendiente (esto es, cómo de rápido se llega al punto máximo de la campana); y, finalmente, c determina el punto más alto de la campana.
Gráficamente la función tiene este aspecto:
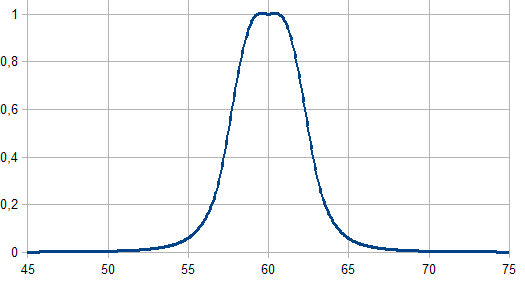
Función Sigmoidal
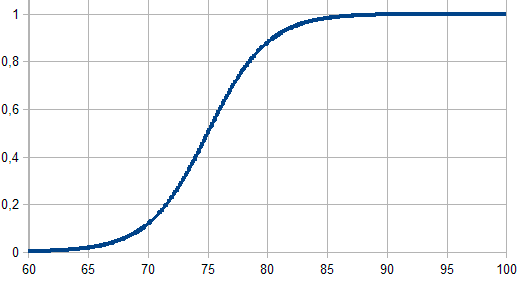
En este caso, la función sigmoidal, similar a la curva logística, sigue la siguiente ecuación:
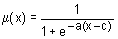
Aquí a determina la pendiente de la función (cómo de rápido pasa de cero a uno) y c determina la coordenada en la que se produce la inflexión de la función (el cambio de signo de la pendiente).
El gráfico de la función sería el siguiente:
Aplicación de Lógica Difusa a un Indicador
Ahora que ya conocemos en detalle las funciones veamos cómo utilizarlas para clasificar los valores de un indicador. Para ello vamos a tomar el Average Directional Movement Index (ADX) estableciendo los siguientes criterios para determinar la fortaleza de la tendencia:
- Tendencia Débil, si el indicador se sitúa entre 30 y 50.
- Tendencia Normal, si el indicador oscila entre 50 y 70.
- Tendencia Fuerte, si el valor del ADX está entre 70 y 100.
Sin embargo, como podemos ver, estos criterios son excesivamente rígidos. ¿Por qué 30-50 para la tendencia débil? ¿Por qué no mejor 20-40? Y si el indicador toma el valor 51, ¿la tendencia tiende más débil o a normal? Aquí es donde entra en juego la lógica difusa para resolver estos problemas. Lo que haremos será asignar los valores que delimitan las diferentes categorías (débil, normal, fuerte) a más de una categoría a la vez, estableciendo diferentes grados de pertenencia.
Para ello, utilizaremos la función trapezoidal para definir tendencia débil, la función gaussiana para representar la tendencia normal y la función sigmoidal para la tendencia fuerte. El resultado de forma gráfica sería el siguiente:
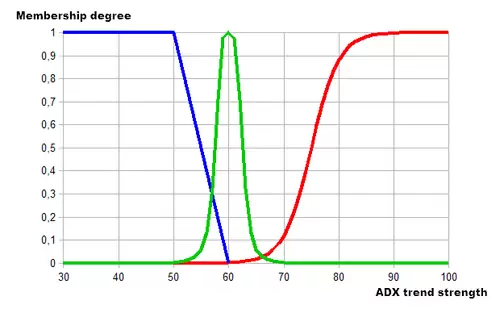
En el gráfico anterior podemos ver que hay áreas que se solapan, mostrando la posible pertenencia a dos categorías. Así, valores entre 50 y 60 pueden ser débiles y normales a la vez, mientras que valores entre 60 y 70 pueden ser normales y fuertes.
Ahora que tenemos definidos los inputs, vamos a definir el output. Dicho de otro modo, vamos a transformar los valores del ADX en reglas prácticas para nuestro trading. Para ello, vamos a determinar el tamaño de las posiciones en base a la fuerza de la tendencia. La idea básica es que cuanto más fuerte sea la tendencia, más riesgo aceptaremos y por tanto mayor será el porcentaje de nuestra cuenta que utilizaremos para abrir posiciones.
En base a esta idea, planteamos tres posibles situaciones:
- Riesgo Bajo -> 2-4% de la cuenta
- Riesgo Normal -> 4-5% de la cuenta
- Riesgo Alto -> 5-10% de la cuenta
Definimos ahora tres funciones de pertenencia para estas categorías:
- Trapezoidal para riesgo bajo
- Triangular para riesgo normal
- Sigmoidal para riesgo alto
El resultado gráfico del output será el siguiente:
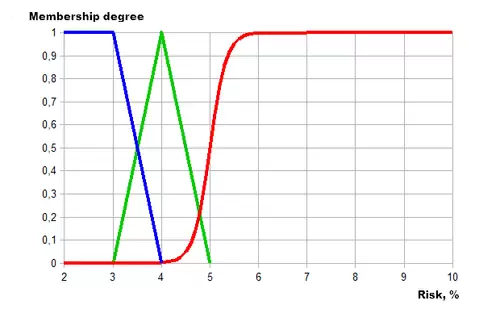
El resultado de todo esto es el siguiente:
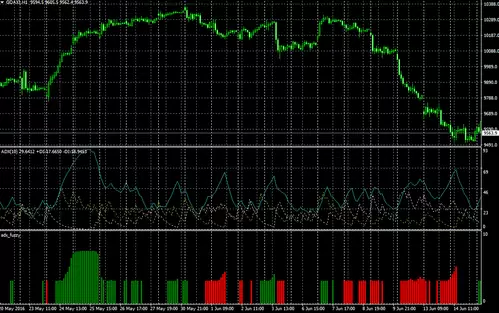
En el gráfico anterior podéis ver el ADX de 10 períodos aplicado al gráfico horario del DAX y justo debajo un histograma que muestra el ratio riesgo/fuerza de la tendencia (verde para alcista, rojo para bajista). Cuanto más alta sea la barra del histograma, mayores posiciones deberemos adoptar en la dirección de la tendencia. La verdad es que visualmente ya de entrada se intuyen entradas muy buenas con este método, por lo que sería interesante crear el Expert Advisor correspondiente para poder testear su funcionamiento.
Si queréis probar el indicador podéis bajarlo desde este hilo del Foro. Recordad que para que funcione antes deberéis instalar la librería FuzzyNet que podéis bajar de la web de MQL5.com o directamente desde el apartado de Metatrader del Foro. No olvidéis que debéis copiar todos los archivos de la librería en la carpeta MQL4/Include/Math/FuzzyNet/.
(Continuará…)
Saludos,
X-Trader