Seguramente hayan oido Vds. hablar de este término pero seguro que muchos desconocen qué es exactamente. Para el que no lo sepa, una martingala es una supuesta fórmula para ganar siempre en los juegos de azar, que consiste en ir aumentando la apuesta según un ritmo dado en caso de pérdida para compensar, con la futura ganancia, las cantidades perdidas hasta el momento.
Para aquellos que les gusten las Matemáticas, diremos que una martingala es una secuencia de variables aleatorias, X1, X2, …, cada una de ellas con media finita, que verifican que la esperanza condicional de Xn+1, dadas X1, X2, …, Xn es igual a Xn tal que:
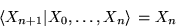
El término «martingala» fue utilizado originalmente para describir esta peculiar forma de apostar en los casinos que se puso de moda en el siglo XVIII (* ), si bien fue introducido en el mundo matemático por Lévy, y desarrollado después por Doob.
Por si no ha quedado claro, veamos el siguiente ejemplo. Sea el juego de azar más sencillo, lanzamos una moneda y obtenemos cara (C) o cruz (+). Apostamos 1 Euro a que sale C. Si sale, hemos ganado 1 €. Si no, apostaremos 2 € en el siguiente lanzamiento. Si perdemos otra vez, no importa, apostamos 4 €. Y si ciertamente tenemos hoy un día de mala suerte y volvemos a perder, apostamos 8 €. Esta vez la suerte nos es favorable y sale C. Ganamos 8 €. Como en las cuatro jugadas anteriores habíamos perdido 1 + 2 + 4 = 7 €, todavía ganamos 1 €.
Es decir: considerando dividido el juego en «rachas» terminadas por C, en cada «racha» ganamos 1 €. Por ejemplo, sea la sucesión:
Si la escribimos así:
fácilmente vemos que se ganan 21 €, uno por cada paréntesis.
Es fácil relacionar todo esto con los mercados financieros y el trading. Basta con que pensemos que el mercado es un gigantesco casino y que las cruces y caras del ejemplo son operaciones de compra y de venta.
Posiblemente, cuando Vds. empiecen en el mundo de la Bolsa se encontrarán con más de uno que les promete el oro y el moro porque tienen el sistema infalible, sobre todo si se trata de un sistema para acciones; una vez que se lo cuenten, verán que no es más que una martingala, mediante la que se dobla el nº de contratos/acciones cada vez que se pierde en una operación. Sin embargo, si este sistema es tan infalible, ¿cómo no desaparecen los casinos y los mercados financieros? ¿Dónde está el fallo de la martingala?
Lo que sucede simplemente es que nosotros operamos con un capital limitado (B), siempre inferior al del mercado. Para simplificar, convenimos en que B = 2^N, es decir, que podemos resistir una «racha» de pérdidas de longitud máxima N. Así por ejemplo, si disponemos de 1024€, una racha de 10 operaciones negativas nos produciría una pérdida igual a esta cantidad, y ya no podríamos seguir operando.
Ciertamente, la probabilidad de que se presente esta racha es pequeña. Dicha probabilidad puede calcularse como p = 1/(2^N), es decir, que por término medio sólo se presentará una vez de cada 2^N. Pero observemos un hecho interesante: nuestra ganancia en cada «racha» ha sido 1 €. Sin embargo, cuando se presente la «racha fatídica» perderemos de golpe todo lo atesorado pacientemente a lo largo de las rachas anteriores. Los 1024 € se esfumarán en un momento, destruyendo el trabajo de horas y horas con el consiguiente impacto psicológico en el trader.
Generalicemos estos resultados: en general, en cualquier juego de azar equilibrado (y aqui debemos suponer que operar en los mercados sigue una lógica similar a la de un juego de azar) a la larga gana siempre el jugador que posea la mayor banca, o, mejor dicho, tiene una probabilidad mayor de arruinar al contrario (es decir, que puede resistir rachas de pérdidas más largas). Observen, volviendo al tema de los juegos del casino lo que sucede si el juego no es equilibrado (es decir, que las probabilidades de que se dé un determinado suceso no son iguales para todos los sucesos). Tomemos el ejemplo de la ruleta. La existencia en ella del cero hace que la probabilidad de ganar en una apuesta a «rojo» o «negro» por ejemplo, no sea p = 0.50, sino p = 18/37 = 0.4865. Esta pequeña diferencia a favor del casino contribuirá a arruinarnos más rápidamente
Para ilustrar la afirmación anterior, vamos a recurrir a las siempre socorridas simulaciones de MonteCarlo. Partimos de los siguientes supuestos:
– Suponemos que operamos intradía en una sesión bursátil cualquiera
– En cada sesión empezamos con un capital de 100.000 €.
– Apostamos 100 € a que el mercado va a bajar, manteniendo fijo el valor si ganamos. Cada vez que perdemos, doblamos la apuesta (salvo si nuestra banca en ese momento es inferior a 100 €; en ese caso apostamos el resto).
Realizamos el estudio para un número variable de «rachas» en cada sesión, siendo cada «racha» una serie de subidas en contra de nuestra posición que culmina con una bajada a nuestro favor. Nuestras ganancias/pérdidas dependerán, por tanto, del número de «rachas» que se nos presente en cada sesión.
|
Nº de Rachas por Sesión
|
Sesiones con Pérdidas
|
Sesiones con Ruina
|
|
100
200 500 1000 2000 5000 |
6.1%
9.8% 21.1% 40.2% 49.3% 64.5% |
3.5%
7.4% 15.4% 27.5% 47.3% 64.4% |
Es decir, que, por ejemplo, si presentan 500 rachas por sesión, en un 21.1% de ellas acabaremos con pérdidas. En ellas están comprendidas el 15.4% del total en que nos arruinaremos totalmente.
Observemos que la técnica de la martingala, si es jugada unas pocas veces, casi nos garantiza una pequeña ganancia, pero a costa de exponer todo nuestro capital. La jugada sería comparable a apostar nuestra vivienda, que vale 200.000 €, contra 20 € en un juego en el que nuestra probabilidad de ganar es p = 0.9999. Si jugamos unas pocas veces, podemos está prácticamente seguros de ganar unos euros, pero no dejaremos de haber expuesto toda nuestra vivienda.
Sin embargo, existen otros métodos para apostar más avanzados que la martíngala:
– Sistema Paroli ó Anti-Martingala: se trata del sistema contrario a la Martingala. Se trata de aumentar el capital que arriesgamos tras una operación ganadora y volver a arriesgar el capital que inicialmente deseábamos arriesgar.
– Sistema 1-3-2-6: se trata una modificación del Sistema Paroli. Consiste en modificar las proporciones que arriesgamos en cada operación. Así, si en la primera operación, arriesgamos 100 €, cuando ganemos en la siguiente operación arriesgaremos 300 €. Cuando ganemos de nuevo, el capital a arriesgar será de 200 €; y finalmente cuando ganemos de nuevo, el capital a arriesgar será ahora de 600 €. Seguidamente volvemos a empezar arriesgando de nuevo 100 €. Asimismo, si tenemos una operación perdedora en cualquiera de los niveles de riesgo (1, 3, 2, 6) volvemos a arriesgar tan sólo 100 € por operación, hasta que tengamos una operación ganadora.
– Sistema D’Alembert: se trata de una mezcla entre sistemas de tipo Martingala y de Seguros. Básicamente aumentamos el capital que arriesgamos en un número fijo de unidades cada vez que perdemos y reducimos el capital que arriesgamos cada vez que ganamos.
– Sistema Labouchere: también denominado Sistema de Cancelación. Consiste en escribir una determinada secuencia de números, por ejemplo, 1, 2, 3, 4, 5, 6 (aunque pueden repetirse números como por ejemplo 1 1 1 3 3 5 5 7). Seguidamente debemos apostar en nuestra primera operación la suma del primer y último número multiplicada por la unidad mínima de capital que queramos arriesgar. Así, si tomamos la primera serie y el capital mínimo a arriesgar es de 100 €, en la primera operación arriesgariamos (1+6) * 100 € = 700 €.
Si ganamos en la primera operación, eliminamos el 1 y el 6 y sumamos los dos siguientes: 2 + 5 = 7 (en este caso, coincide el resultado pero con otras series los resultados varían). Volvemos a multiplicar por la unidad base. So volvemos a ganar, repetimos el proceso y así sucesivamente hasta que se termine la serie. Cuando se acabe, volvemos a empezar de nuevo.
Si perdemos en la primera operación, entonces añadimos 1+6 = 7 a la serie inicial de tal forma que obtenemos la siguiente serie: 1, 2, 3, 4, 5, 6, 7. Y aplicamos el proceso anterior: sumamos 1 + 7 = 8, que multiplicado por la unidad base nos da 800 € que debemos arriesgar en la siguiente operación.
En cualquier caso, se verifica que siempre que se termina la serie, obtendremos beneficios.
– Sistema Parlay: basado en el sistema Anti-Martingala, consiste en aplicar dicha técnica con la particularidad de que en queda operación se reinvierten los beneficios en las operaciones ganadoras.
– Sistema Ormond: arriesgamos una cantidad inicial, N. Si ganamos arriesgamos la misma cantidad; si perdemos, arriesgamos (1+x)*N en la siguiente operación siendo x el número de operaciones perdedoras que hayamos tenido en la última racha.
– Sistema Winner’s Edge: variación del Sistema Labouchere. Cuando ganamos sumamos el primer y último número en la primera operación y después 3 números de la secuencia (dos primeros y último, ó primero y dos últimos) hasta que perdamos. Si perdemos añadimos al final de la secuencia la suma de los números y multiplicamos el capital mínimo por el primer número de la serie; si perdemos de nuevo, arriesgamos únicamente el capital mínimo sin multiplicar hasta que ganemos. Se recomienda comenzar utilizando un capital total de 40 x Nº Inicial de la serie x Capital Mínimo.
Dejamos al lector que reflexione y medite sobre estas estrategias y si su aplicación al trading es útil o presentan falacias similares a las de la Martingala…
X-Trader
(*) Según Alexey de la Loma (ver artículo), existen dos teorías sobre el origen del término Martingale; según la primera, proviene de un pueblo del sur de Francia llamado Martigues, cuyos habitantes han tenido siempre fama de extravagantes y por eso a la forma de jugar en el casino doblando la apuesta tras una pérdida se denominó «à la martingale», que se identificaba como «de forma absurda». Según otras fuentes proviene de un famoso jugador que en el siglo XIX frecuentaba los casinos de la Riviera Francesa.