Ahora que hemos entendido que las dimensiones espaciales no tienen porque ser números enteros, ¿qué impacto tiene en la forma que tenemos de medir los contornos? En esta entrega veremos la importancia de la dimensión de Hausdorff en nuestra concepción del espacio y el tiempo, así como en su medida.
Un Mundo Peligroso
Muchas cosas en la vida son aleatorias. Se rigen por la probabilidad, por casualidad, por azar, por accidente, por el dios Hermes, por la fortuna. Así que las medimos por la probabilidad, usando nuestra jarra de mermelada, tal y como vimos en el artículo anterior.
Los lugares donde hay más mermelada son más probables, si bien el siguiente resultado siempre es incierto. El siguiente resultado podría ser un evento de baja probabilidad. O podría ser un evento de alta probabilidad, pero puede haber más de uno de estos.
La desintegración radiactiva se mide mediante la probabilidad. El momento de la transformación espontánea de un núcleo (en la cual se emite radiación, pierde electrones, o se somete a la fisión) no se puede predecir con certeza.
A algunas personas no les gusta este aspecto del mundo. Prefieren creer que hay «variables ocultas» que realmente determinan la desintegración radiactiva, y si sólo supiéramos cuáles son esas variables ocultas, todo sería predecible de forma precisa, y se podría volver al paraíso de un universo de Laplace.
Sin embargo, esas “variables ocultas” posiblemente no sea más que otro nombre para la probabilidad. «¿Fue un accidente?» «No, fue causado por las fuerzas ocultas.» Todos los teóricos de las variables ocultas creen en la conspiración.
Lanzamientos de Moneda y Movimiento Browniano
Podemos crear una especie de movimiento browniano lanzando monedas. Comenzamos con una variable x = 0. Lanzamos una moneda. Si sale cara, le sumamos 1 a x. Si sale cruz, le restamos 1 a x. Si denotamos el valor de entrada como x(n) y el valor de salida como x(n + 1), obtenemos un sistema dinámico:
x(n+1) = x(n)+1, con una probabilidad p = 0.5
x(n+1) = x(n)-1, con una probabilidad de q = 1-p = 0.5
Aquí n representa el número de lanzamiento de moneda actual, y es nuestra medida del tiempo. Para crear un gráfico de este sistema, ponemos n (tiempo) en el eje horizontal, y la variable x(n) en el eje vertical. Con esto conseguimos un gráfico muy sencillo del movimiento browniano (un paseo aleatorio), como se ve en el siguiente gráfico. En cualquier punto en el tiempo (en cualquier valor de n), la variable x(n) representa el número total de caras menos el total de cruces. Aquí está una imagen mostrando 10.000 lanzamientos de la moneda:
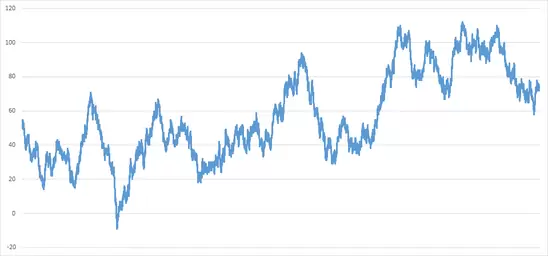
Hmmm, ¿a qué me recuerda ese gráfico? 😛
Gran parte de modelos utilizados en los mercados financieros se basa en un simple modelo de probabilidad como éste. Más adelante vamos a cambiar este modelo, cambiando la forma en que medimos la probabilidad.
Un Sencillo Fractal Estocástico
Usando la probabilidad, es fácil crear fractales. Por ejemplo, aquí tenemos un sistema dinámico que crea un fractal estocástico simple. El sistema cuenta con dos variables, X e Y, como entradas y salidas:
x(n+1) = -y(n)
y(n+1) = x(n)
con probabilidad p = 0.5, pero además:
x(n+1) = 1 + 2.8*(x(n)-1)/(x(n)*x(n)-2*x(n)+2+y(n)*y(n))
y(n+1) = 2.8*y(n)/(x(n)*x(n)-2*x(n)+2+y(n)*y(n))
con probabilidad q = 1-p = 0.5
Después de varias iteraciones, si representamos x e y en un gráfico de dos dimensiones obtenemos un resultado como el siguiente:

Los sistemas dinámicos estocásticos simples crean fractales simples, como los que vemos en la naturaleza y en los mercados financieros. Sin embargo, con el fin de pasar de Bachelier de Mandelbrot, lo cual requiere un cambio en la forma en que medimos la probabilidad, nos será útil pensar primero en algo más simple, como la forma en que medimos la longitud.
Una vez hayamos aprendido a medir la longitud, veremos que la probabilidad no es más que mermelada sobre una tostada.
[Si desean jugar con los gráficos anteriores, pueden descargar la hoja de cálculo con la que los he generado haciendo click aquí]
Revisitando Sierpinski y Cantor
En el primer artículo de la serie, cuando examinamos la alfombra de Sierpinski, vimos que esta tenía una dimensión de Hausdorff D = log 8 / log 3 = 1.8927… Así que si tenemos una alfombra de Sierpinski con una longitud de 10 metros por cada lado, obtenemos N = rD = 10D = 101.8927 = 78.12 copias más pequeñas del original. (Si queremos obtener un número redondo, podemos usar 9 metros por cada lado, obteniendo N = 91.8927 = 64 copias más pequeñas). Puesto que cada una de estas copias más pequeñas tiene una longitud de un metro por cada lado, podemos llamar a esta nueva unidad «metros cuadrados». Pero en realidad se trata de «Sierpinskis cuadrados», porque la alfombra de Sierpinski no es como una alfombra ordinaria.
Dicho esto, nos preguntamos: ¿cuánto espacio (área) toma la alfombra de Sierpinski en relación a una alfombra ordinaria? Tenemos 78.12 copias más pequeñas del original. Así que si conocemos la cantidad de área (en términos de la alfombra ordinaria) que cada una de estas copias más pequeñas ocupa, podemos multiplicar ese número por 78.12 y obtener la respuesta.
Antes de hacer el cálculo para la alfombra de Sierpinski, recordemos lo que hicimos con el polvo de Cantor en el artículo anterior: tomamos una línea de longitud uno y empezamos a cortar agujeros en ella. La dividimos en tres partes y retiramos la parte central, tal que:
0__________________________________________________1
0 ________________ 1/3 2/3_______________ 1
Eso nos deja 2/3 de la longitud original. A continuación, retiramos los tercios medios de cada una de las dos líneas restantes, dejando 2/3 de lo que había antes; es decir, (2/3) x (2/3) = (2/3)2, y así sucesivamente. Después de la etapa n-ésima de retirar tercios medios, la longitud de la línea restante es (2/3)n.
Si tomamos el límite cuando n tiende a infinito, tenemos que (2/3)n tiende a 0 (es decir, seguimos multiplicando la longitud restante por 2/3, y al hacerlo, eventualmente reducimos la longitud restante a cero). Así que el polvo de Cantor tiene una longitud de cero. Lo que queda es un número infinito de puntos desconectados, cada uno con dimensión cero. Por lo que dicho polvo de Cantor tenía una dimensión topológica de cero. A pesar de que empezamos con un segmento de recta con dimensión 1, antes de comenzar a hacer cortes en ella.
Bien. Ahora vamos a hacer lo mismo con la alfombra de Sierpinski. Tenemos un cuadrado y dividimos sus lados en tres partes (dividir por un factor de escala de 3), lo que genera 9 cuadrados más pequeños. Luego quitamos el cuadrado de enmedio, dejando 8 cuadrados más pequeños, como en la figura siguiente:

Así que nos quedan 8/9 de la superficie original. A continuación, dividimos cada uno de los cuadrados más pequeños, y quitamos los centros. Cada uno de ellos tiene ahora 8/9 de su superficie original, por lo que el área del cuadrado grande se ha reducido a (8/9)x(8/9) de su tamaño original, es decir, (8/9)2. En la etapa de orden n de este proceso, hemos dejado (8/9)n de la superficie original. Tomando el límite cuando n tiende a infinito, tenemos (8/9)n tiende a 0. Así que la alfombra de Sierpinski tiene una superficie de cero.
¡Vaya! Ahora resulta que las 78.12 copias más pequeñas de la alfombra de Sierpinski original que mide 10 x 10 (o 64 copias más pequeñas de una alfombra de Sierpinski original que mide 9 x 9), en realidad ocupan cero. Al menos si consideramos esta forma de medir las cosas.
¿A qué se debe esto? Si nos fijamos nuevamente en la forma de construir la alfombra, podemos observar que el perímetro exterior del cuadrado original nunca es perforado a medida que creamos la alfombra de Sierpinski, de tal forma que el perímetro exterior forma una línea cerrada en forma de cuadrado cuya dimensión es uno.
Asimismo podemos ver que el borde del primer cuadrado central también permanece intacto. Esto deja una segunda línea cerrada de dimensión uno, dentro de la secuencia original. A continuación, los centros de los 8 cuadrados más pequeños también forman bucles (cuadrados) aún más pequeños. Si seguimos este proceso hasta el infinito, en el límite nos quedamos con un número infinito de ciclos desconectados, cada uno de los cuales es una línea de una dimensión. Esta es la alfombra de Sierpinski.
Ahora bien, con respecto al polvo de Cantor, dijimos que estaba compuesto por un número infinito de puntos desconectados, cada uno con dimensión cero, por lo que dijimos que si el propio polvo de Cantor tenía una dimensión topológica de cero. Para ser coherentes, habría que decir con respecto a la alfombra de Sierpinski, la cual se compone de un número infinito de bucles desconectados de dimensión uno, que tiene una dimensión topológica de uno.
Esto parece que empieza a complicarse. En los artículos anteriores habíamos dicho que la alfombra de Sierpinski tenía una dimensión ordinaria (o topológica) de 2 (¿recuerdan que intentábamos cubrir el suelo de una habitación cuadrada?).
La confusión radica en el tipo de dimensión que estemos considerando: sabemos con seguridad que la dimensión euclídea de la alfombra es de 2 ya que el suelo que queremos cubrir es un plano de 2 dimensiones. Pero, una vez que medimos todos los agujeros en la alfombra, descubrimos que lo que queda es un número infinito de bucles cerrados desconectados, cada uno de los cuales tiene una dimensión igual a 1. Por lo tanto, en este sentido, vamos a decir que la alfombra de Sierpinski tiene una dimensión topológica de 1.
Resumiendo, ahora tenemos tres dimensiones diferentes para la alfombra de Sierpinski: una dimensión euclídea (E) de 2, una dimensión topológica (T) de 1, y una dimensión de Hausdorff (D) de 1.8927…
Del mismo modo, en el caso del polvo de Cantor, diremos que tiene una dimensión euclídea (E) de 1, una dimensión topológica (T) de 0, y una dimensión de Hausdorff (D) de log 2/log 3 = 0.6309…
Es decir, hay tres maneras diferentes de mirar la misma cosa: la dimensión euclídea (E), la dimensión topológica (T) y la dimensión de Hausdorff (D). Pero, ¿cuál es la mejor?
Las Medidas Inútiles no son Buenas
Hace tiempo leí sobre una tribu primitiva que tenía un sistema de conteo que era el siguiente: 1, 2, 3, muchos. Es decir, no había nombres para los números más allá de 3. Así decían:
«¡Estamos siendo invadidos por extranjeros!»
«¿Cuántos de ellos hay?»
«¡Muchos!»
No es muy buen sistema de numeración, ya que no permite distinguir entre una fuerza invasora de cinco y una fuerza invasora de cincuenta.
«Muchos». Inútil. Otras dos medidas “inútiles” son cero e infinito. Por ejemplo, la alfombra de Sierpinski tiene un área de cero y lo mismo ocurre con el polvo de Cantor. Pero no son la misma cosa.
Podemos obtener un poco más de información si sabemos que el polvo de Cantor tiene una dimensión topológica de cero, mientras una alfombra de Sierpinski tiene una dimensión topológica de uno. Pero la topología a menudo oculta más de lo que revela. La dimensión topológica de cero no nos dice cómo el polvo de Cantor se diferencia de un solo punto. La dimensión topológica de uno no nos dice cómo una alfombra de Sierpinski se diferencia de un círculo.
Si tenemos un círculo, por ejemplo, es bastante fácil de medir su longitud (L). De hecho, sólo basta con conocer la longitud del radio r y usar la siguiente fórmula:
L = 2·Pi·r
Pero supongamos que intentamos medir la longitud de una alfombra de Sierpinski. Después de todo, hemos dicho que una alfombra de Sierpinski tiene dimensión topológica de uno, como una línea, por lo que, ¿cuál es la longitud de esta alfombra de Sierpinski en comparación con la longitud de una circunferencia?
Para medir la alfombra de Sierpinski comenzamos la medición de cuadrados cada vez más y más pequeños, por lo que nuestra “vara de medir” debe ser cada vez más pequeña. Pero como los cuadrados se hacen más pequeños, hay más y más de ellos. Si realmente tratamos de hacer la medición, descubriremos que la longitud tiende a infinito. Otra vez una medida inútil.
El Perímetro de las Costas y las Curvas de Koch
Si nos fijamos en los datos oficiales de la longitud de las fronteras entre países, como la que existe entre España y Portugal, o la que separa Bélgica y los Países Bajos, encontrará que puede haber variaciones de hasta un 20 por ciento.
¿A qué se debe esto? Sencillamente a que utilizan varas de medir de diferentes longitudes. Si medimos las cosas con una vara de medir de longitud m, la ponemos junto a lo que queremos medir, marcamos el punto final de la vara, y repetimos el proceso hasta que tengamos N longitudes medidas, tendremos que la longitud total L del objeto es L = m·N
Por ejemplo, supongamos que estamos midiendo las cosas en metros, y tenemos una vara de longitud m = 3. Deseamos medir la longitud de las pistas de un polideportivo por lo que vamos colocando la vara a lo largo de las pistas, obteniendo N = 100. La longitud total es de L = 3·100 = 300 metros.
Si en su lugar utilizamos una pequeña vara de medir, por ejemplo una regla de longitud m = 1 y obtenemos N = 300, la longitud seguirá siendo la misma, esto es, L = 1 · 300 = 300 metros. Esto puede servir para el lado de unas pistas deportivas pero, ¿funciona para la costa de Gran Bretaña? ¿Y para la longitud de la frontera entre España y Portugal?
Portugal es un país más pequeño que España, por lo que, lógicamente, utilizó una vara de medir más corta, obteniendo una estimación de la longitud de la frontera común más larga que la estimación realizada por España.
Podemos ver el motivo fácilmente si suponemos que queremos medir, por ejemplo, la costa de Gran Bretaña. Si tomamos un mapa, tiramos una cuerda a lo largo de la costa oeste de Gran Bretaña, y multiplicamos el resultado por la escala del mapa, obtendremos una estimación de la «longitud» de la costa occidental. Pero si bajamos de nuestra vista por satélite y visitamos la costa en persona, veremos que hay una gran cantidad de entradas y salidas y retorcidos dientes de sierra en las zonas donde el mar se encuentra con la tierra. Cuanto menor es la vara de medir que utilicemos, más larga será nuestra medida, porque capturaremos con más detalle la longitud de las irregularidades. La diferencia entre una costa y el lado de una pista deportiva es que la costa es fractal y el lado del campo de fútbol no.
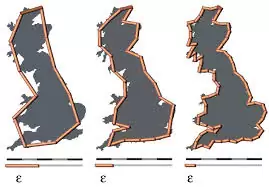
Para ver los principios involucrados en ello, vamos a jugar con algo llamado curva de Koch. En primer lugar vamos a construirla para a continuación medir su longitud. Para hacernos una idea rápida, podemos pensar que una curva de Koch es como una sección de una costa.
Tomamos un segmento de longitud L=1. Ahora lo dividimos en tres partes (cada uno de longitud 1/3), y reemplazamos el tercio medio, con dos segmentos de línea (cada uno de longitud 1/3), que pueden ser considerados como los otros dos lados de un triángulo equilátero.
En este momento tenemos 4 segmentos más pequeños, cada uno de longitud 1/3, por lo que la longitud total es de 4 x 1/3 = 4/3. A continuación repetimos este proceso para cada uno de los 4 segmentos de línea más pequeños. Esto nos da 16 segmentos aún más pequeños, cada uno de longitud 1/9. Así que la longitud total es ahora de 16/9 o (4/3)2. Gráficamente los pasos que acabamos de ver para la construcción de la curva de Koch tienen este aspecto:
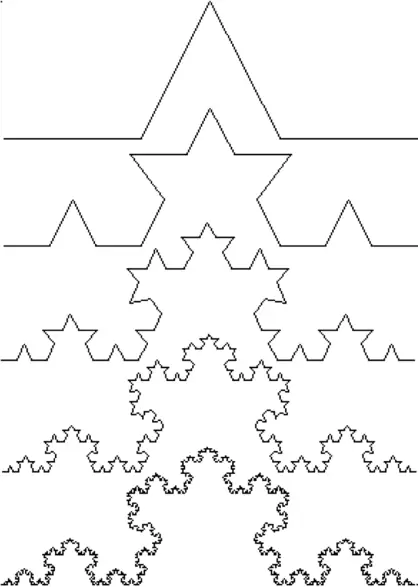
En la fase n-ésima, la longitud será igual a (4/3)n, de tal forma que cuando n tiende a infinito, también lo hace la longitud L de la curva.
Sin embargo, la curva de Koch es continua, porque somos capaces de recorrer su longitud con un lápiz sin levantarlo, de un extremo a otro. Por lo tanto, desde el punto de vista topológico, la curva de Koch tiene una dimensión 1, al igual que la línea original. O, dicho de otro modo, podemos deformar el segmento original sin romperlo por lo que el resultado sigue siendo una «línea».
Para calcular su dimensión de Hausdorff, observamos que en cada etapa de su construcción, reemplazamos cada segmento de línea con n = 4 segmentos, después de dividir el segmento original por el factor de escala r = 3. Por lo que su dimensión de Hausdorff es log 4 / log 3 = 1.2618 …
Por último, cuando construimos la curva de Koch, lo hicimos mediante la visualización en un plano euclídeo de dos dimensiones (sustituimos cada segmento de línea media con los otros dos lados de un triángulo equilátero, lo cual es una figura de 2 dimensiones.) Así que nuestro espacio de trabajo es la dimensión euclídea E = 2.
Pero aquí viene lo interesante: como nuestra vara de medir cada vez es más pequeña (a través de divisiones repetidas por 3), la longitud medida de la línea es cada vez mayor y mayor, al igual que sucedía con la línea de costa. La longitud total (4/3)n se va a infinito a medida que n tiende a infinito. En la etapa de orden n de la construcción tenemos N = 4n segmentos, cada uno de longitud m = (1/3)n, por lo que la longitud total L es:
L = m·N = (1/3)n4n = (4/3)n
El problema de medir de esta manera es el que comentábamos antes: Infinito, «muchos», no es una buena medida.
Si nos preguntamos qué es más largo, la costa de Gran Bretaña o la costa de Francia, no podemos saberlo realmente porque ambas son infinitas si usamos esta medida. O tal vez tienen la misma longitud, quién sabe. Ambas son «muchos» de largo.
Utilizando una Medida de Hausdorff
El problema radica en nuestra vara de medir de longitud m. Tenemos que hacer algo para solucionar el problema de que a medida que m se hace más pequeño, la longitud L se hace más larga. Vamos a intentar lo siguiente. En lugar de usar L = m·N, vamos a ajustar m elevándolo a alguna potencia d. Es decir, ahora L = md·N.
Esto cambia nuestra forma de medir la longitud L, porque sólo cuando d = 1 logramos la misma medida de longitud que antes.
Si hacemos esto, sustituir m por md, descubrimos que para valores de d muy pequeños, L todavía tiende a infinito. Para valores de d que son grandes, L tiende a cero. Siguen siendo malas medidas. Afortunadamente sólo hay un valor de d que es correcto. ¿Lo adivinan? Exacto, es la dimensión de Hausdorff, tal que d = D. Así que nuestra medida de longitud se convierte en:
L = mD·N
¿Cómo funciona esto aplicándolo a la curva de Koch? Hemos visto que para una curva de Koch el número de segmentos de línea en la etapa n es N = 4n, mientras que la longitud del segmento es m = (1/3)n. Por lo que tenemos que la medida de longitud L para la curva de Koch (siendo D = log 4 / log 3):
L = mD·N = ((1/3)n)D·(4n) = ((1/3)n)log 4/log 3·(4n) = 4-n4n = 1.
¡Bien!. Hemos conseguido deshacernos de las medidas inútiles. La longitud L de la curva de Koch en virtud de esta nueva medida resulta ser la longitud del segmento de línea original. Es decir, L = 1.
La dimensión de Hausdorff D es una medida natural asociada con nuestra vara de medir m. Si estamos midiendo las pistas de un polideportivo, usar D = 1 funciona muy bien para medir 100 metros. Pero si estamos tratando con curvas de Koch o costas, entonces algún otro valor de D evita el ejercicio inútil de que la longitud medida dependa totalmente de la longitud de la vara de medir.
Veamos ahora cómo calcular la longitud de una alfombra de Sierpinski construida a partir de un cuadrado con una longitud inicial de 1 en cada lado. Para la alfombra de Sierpinski, N se multiplica por 8 en cada etapa, mientras que la vara de medida se divide por 3. Por lo tanto la longitud en la etapa n es:
L = mD·N = ((1/3)n)D·(8n) = ((1/3)n)log 8/log 3·(8n) = 8-n·8n = 1.
¡Bravo! Volvemos a obtener una longitud finita. No es cero y no es infinito. En virtud de esta medida, a medida que avanzamos desde el cuadrado original a la alfombra de Sierpinski, la longitud se mantiene igual. La longitud (área) de Hausdorff de una alfombra de Sierpinski es 1, suponiendo que empezamos con un cuadrado de lado igual a 1.
Si por el contrario tenemos una alfombra de Sierpinski de lado 9, para calcular el «area», observamos que el número de copias de Sierpinski del cuadrado inicial que tiene un lado de longitud 1 es (dividiendo cada lado en r = 9 partes) N = rD = 91.8927… = 64. Del mismo modo, una alfombra de Sierpinski con 10 cuadrados en cada lado tendrá un «área» de N = 101.8927… = 78.12, etc.
La dimensión de Hausdorff, D = 1.8927…, está más cerca de 2 que a 1, por lo que tener un «área» de 78.12 (que está próximo a un área de 102 = 100 metros cuadrados) para una longitud lateral de 10 es más agradable estéticamente que decir que el «área» es cero.
Esta manera de ver las cosas nos permite no tener que decir de dos alfombras de Sierpinski (uno de lado 9 y otra de lado 1) son exactamente iguales porque tienen área cero y longitud infinita.
¿Y Ahora Qué?
Ahora que conocemos la utilidad de la dimensión de Hausdorff en la medida de las cosas, ¿podemos pensar que los expertos en finanzas se autoengañan porque utilizan la dimensión equivocada para sus cálculos? Recordemos que en el segundo artículo de la serie vimos que, siguiendo a Bachelier, la probabilidad de la distribución del logaritmo del precio varía con la raíz cuadrada del tiempo.
Pero, ¿es D=0.5 la dimensión apropiada para el tiempo? ¿O puede tomar D otros valores diferentes? A esto se refería Mandelbrot cuando decía que la distribución empírica de las variaciones del precio era «demasiado apuntada» como para proceder de una distribución Normal, porque la dimensión D = 0.5 sólo es adecuada en el contexto de una distribución normal, que surge de movimiento browniano simple. Más sobre esto en la próxima entrega de la serie.
(Continuará…)
Saludos,
X-Trader