A petición de Rafa7 os traduzco una serie de artículos publicada en Museful en la que de forma muy elegante se explica cómo derivar el criterio de Kelly y su relación con la entropía de Shannon. Precisamente a raíz de estos artículos, Rafa7 ha subido al Foro una excelente hoja de cálculo para simular diferentes escenarios en base a las ecuaciones presentadas aquí, la podéis descargar visitando este hilo.
¿Cuál es la exposición óptima que un trader debe adoptar en cada operación? En este artículo os explicamos cómo determinarlo de forma matemática. Pero antes de explicaros cómo calcularlo debemos presentar algunos conceptos matemáticos necesarios para que podáis seguir la explicación.
La Función de Utilidad de la Riqueza
A menudo se parte del supuesto que la utilidad de la riqueza es lineal. Por ejemplo, damos por sentado que el valor de 2 € es el doble de 1 €. Sin embargo, en el mundo real ese supuesto no se verifica por cuanto la cantidad de riqueza disponible es finita.
Supongamos el caso de tres individuos idénticos que se diferencian por la renta que tienen disponible:
- El individuo A tiene 2.000 €
- El individuo B tiene 1.000 €
- El individuo C no tiene dinero
Comparando la situación de los tres está claro que el individuo A está mejor que el B, pero claramente el individuo B está mucho mejor que el C. La situación de B es claramente mejor que el punto medio situado entre la utilidad del individuo A y el individuo C. Los primeros 1.000 euros son una necesidad, mientras que los siguientes 1.000 son comodidad.
Por supuesto, la forma exacta de la función de utilidad de la riqueza depende mucho del contexto (¿quién es el propietario de la riqueza? ¿Qué objetivos tiene el propietario?, etc.). No obstante, en términos generales y considerando la utilidad de la riqueza en una variedad amplia de contextos, sabemos que la función será:
- Monótona no decreciente, porque tener más riqueza nunca es malo.
- Cóncava a gran escala, debido a que los rendimientos derivados de un aumento de la riqueza son decrecientes.
La forma de la función podría ser, por ejemplo, algo como lo siguiente:
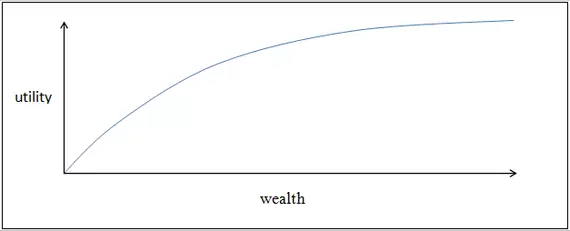
El hecho de que la función de utilidad de la riqueza sea no lineal nos sirve como base para entender una variedad de principios intuitivos en múltiples campos, desde la política a la gestión de riesgos. Por ejemplo, vamos a utilizar el tipo de función que acabamos de derivar para explicar por qué apostar no es racional.
La mayoría de la gente considera que apostar (incluso aún con las probabilidades a nuestro favor) no es racional. Este argumento intuitivo descansa sobre una sólida base matemática: si bien un juego con las probabilidades equilibradas produce una variación nula en nuestra riqueza esperada, puede suceder que la variación que ello provoca en nuestra utilidad sea negativa.
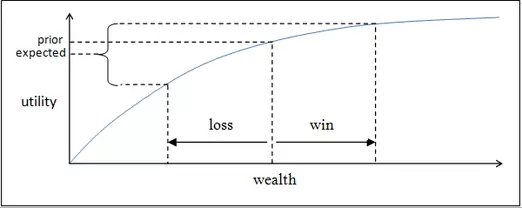
Por este motivo, jugar a un juego justo es peor que no jugarlo. Si la función de utilidad de la riqueza fuera lineal, un juego justo sería una acción neutral en lugar de una decisión absurda.
La Función de Utilidad del Trader
Pasemos a examinar un caso más concreto: consideremos el caso de un trader racional, un trader que no tiene emociones en relación a su cuenta, y cuyo objetivo es maximizar el crecimiento de su capital en el largo plazo. Para este trader, suponiendo que su cuenta tiene un tamaño tal que no tiene poder para influir en el mercado, será igualmente difícil alcanzar un cierto porcentaje de crecimiento en una cuenta pequeña que en una cuenta grande.
Para representar este comportamiento utilizaremos una función de tipo logarítmico, esto es, vamos a establecer que relación existente entre utilidad y tamaño de la cuenta es logarítmica. Gráficamente el aspecto de tal función es el siguiente:
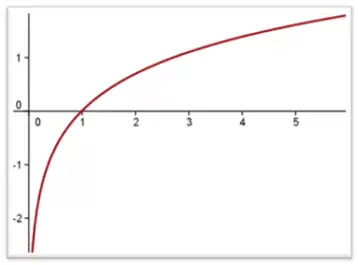
Analizando el gráfico anterior podemos decir que:
- Una pérdida del 1% equilibra un beneficio del 1%.
- Una pérdida del 5% equilibra un beneficio del 5.3% (porque 0.95×1.053 = 1).
- Una pérdida del 10% equilibra un beneficio del 11% (porque 0.90×1.11 = 1).
- Una pérdida del 20% equilibra un beneficio del 25% (porque 0.80×1.25 = 1).
- Una pérdida del 50% equilibra un beneficio del 100% (porque 0.50×2.00 = 1).
Dicho de otro modo, mediante esta curva estamos modelizando el conocido como “apalancamiento asimétrico”: una ganancia del 20% no permite recuperar una pérdida del 20%, motivo por el cual aceptar una apuesta con probabilidad de acierto del 50% y ganancia del 20% en caso de acertar es una mala idea: terminaríamos perdiendo en el largo plazo. Tan solo tendrá sentido aceptar la apuesta cuando tengamos unas probabilidades suficientemente a nuestro favor. La pregunta ahora es: ¿cuándo estarán “suficientemente” a nuestro favor? Lo estarán cuando el cambio esperado en nuestra utilidad (en lugar del cambio esperado en la riqueza) sea positivo.
Si han seguido el razonamiento hasta aquí, ahora podemos expresar esto visto desde el punto de vista de un trader racional: ¿cuánto riesgo (exposición) debemos asumir en una determinada operación, de la que sé previamente la probabilidad de que acierte? Para calcularlo, bastará con maximizar la utilidad esperada con respecto al tamaño de la posición.
Optimizando la Exposición
Consideremos una operación típica, la cual presenta dos posibles resultados: tras abrir la posición, el mercado puede moverse a nuestro favor y alcanzar el objetivo de beneficios, o moverse en nuestra contra y tocar el stop de pérdidas. En cualquiera caso, al alcanzar un determinado nivel la posición se cierra y se asume el correspondiente beneficio o pérdida.
Definimos p como la probabilidad de ganar considerando al mercado como eficiente (es completamente impredecible, comportándose como un paseo aleatorio). Por tanto, 1-p será la probabilidad de perder bajo las mismas condiciones.
Si el mercado es completamente eficiente, entonces operar en él será similar a apostar, siendo la esperanza matemática de este juego igual a cero (suponiendo que no existen spreads y comisiones). Es decir:
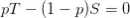
Donde T es el objetivo de beneficio y S el stop de pérdida, ambos valores positivos y considerados en relación al punto de entrada. Despejando p tenemos que:
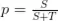
Dicho en términos llanos, la expresión obtenida para p nos indica la “creencia del mundo exterior” que se tiene para la probabilidad de ganar dada una operación abierta. Sea b nuestra propia creencia acerca de la probabilidad de ganar. Si consideramos que el mercado es realmente eficiente, estaremos de acuerdo con la creencia externa y, por lo tanto, b=p. Pero si creemos que el movimiento del mercado estará sesgado a nuestro favor entonces se cumplirá que b>p.
Pasamos a definir las siguientes variables:
- x es el tamaño de la cuenta.
- y es la utilidad que proporciona la cuenta.
- f es la fracción (o múltiplo) del tamaño de cuenta que invertiremos en una operación (acotado por el apalancamiento disponible).
- m es el precio de apertura de la posición.
- s es el spread y las comisiones (expresado en las mismas unidades que m).
- ∆… denota la variación experimentada por la cuenta como resultado de la operación.
- E{…} es la esperanza matemática (media ponderada por probabilidad).
Comenzamos con la optimización: partimos de la función de utilidad logarítmica de la riqueza:
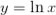
La utilidad de la cuenta tras cerrar la operación será:
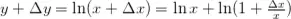
Por lo que la variación de la utilidad será:
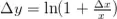
La variación porcentual de la cuenta será:
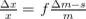
Sustituyendo en la expresión anterior queda:
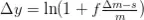
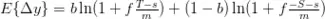
A fin de determinar la exposición óptima, necesitamos maximizar E{∆y} con respecto a f. Si E{∆y}<0 entonces la posición no debería abrirse en ningún caso.
Para calcular el máximo debemos buscar el punto estacionario de la función igualando la derivada primera a cero:
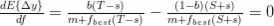
Obteniendo que:
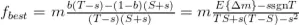
El resultado responde a nuestra cuestión inicial: cuánta exposición debemos tomar al abrir la posición. Dicho resultado será solo válido siempre que |E{∆m}|>s. De lo contrario, se cumpliría que E{∆y}<0.
Adicionalmente si se cumple que el spread y las comisiones son despreciables podemos aproximar la expresión obtenida tal que:
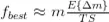
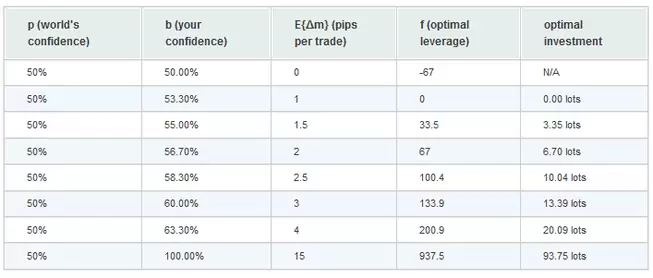
Veamos una aplicación práctica de este resultado. Para ello vamos a asignar valores a las diferentes variables:
- Operamos en EURUSD el cual suponemos que cotiza a 1.5000
- Tenemos una cuenta de 10.000 dólares (0.1 lotes).
- Nuestro take profit y stop los son iguales a 15 pips.
- El total es spread y comisiones es igual a 1 pip.
Variando los valores de b y |E{∆m}| obtenemos diferentes porcentajes de cuenta en base a la expresión obtenida para f:
La Importancia de la Información
Analizando la tabla anterior podemos ver que para obtener un resultado positivo necesitaremos tener una probabilidad de ganancia superior a la que nos otorga el mercado. Y para ello necesitaremos contar con un conjunto de información que nos permita mejorar nuestro trading. Por ello, vamos a probar que existe una relación entre rentabilidad e información.
En particular, vamos a ver que para una operación con TP y SL fijos, la ganancia de utilidad óptima esperada será igual a la ganancia de información en relación a la creencia externa. Dicho de otro modo:
- 1 bit de “información interna” puede doblar la cuenta (21).
- 0.5 bits pueden ofrecer el crecimiento de la utilidad esperada equivalente a un crecimiento del 41% de la cuenta (20.5).
- 0.1 bits pueden ofrecer el crecimiento de la utilidad esperada equivalente a un crecimiento del 7% de la cuenta (20.1).
- Etc.
Veamos la demostración de esta afirmación. Para ello consideraremos que:
- Solo hay dos posibles resultados (TP, SL).
- p es la probabilidad de ganar en un mercado eficiente (creencia externa).
- b es la probabilidad de ganar de acuerdo con las creencias del trader.
Como hemos visto anteriormente, que el mercado sea eficiente implica que:
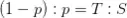
Asimismo, definimos r como una variable proporcional a la inversión realizada (exposición adoptada) para cada operación, tal que cuando ganamos obtenemos r(1-p) del tamaño de la cuenta mientras que cuando perdemos, la pérdida equivale a rp de la cuenta.
Por último, debemos presentar el concepto de información de Shannon. Para ello utilizaremos un sencillo ejemplo: consideremos el lanzamiento de una moneda (50% de probabilidad para cada caso). Dicho lanzamiento genera un dígito binario (bit) de información de Shannon en cada lanzamiento. Si supiéramos que la moneda está trucada, entonces tendríamos una cantidad de información generada menor porque una fracción de la información es conocida antes de que se lance la moneda. Dicho de otro modo:
Información Previa = Información Total (1 bit) – Información sobre el Lanzamiento (Entropía)
Si consideramos el caso de nuestra operativa, la información previa a la operación vendrá dada por:
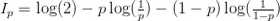
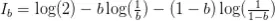
Ip es la información conocida por el mercado eficiente acerca del resultado de nuestra operación en el momento de abrirla, mientras que Ib es la información conocida por el trader (si la información es correcta).
La utilidad posterior, suponiendo que la función de utilidad es logarítmica, de acuerdo con la creencia del trader viene dada por:
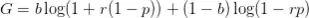
Maximizando esta expresión con respecto a r obtenemos que:
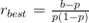
Y, por tanto:
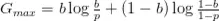
Expresión conocida como divergencia de Kullback-Leibler (también conocida como ganancia de información, divergencia de información o entropía relativa), y mide el «desacuerdo» en la información entre el trader y el mercado eficiente. Dicho de otro modo, esta expresión nos muestra la diferencia en información, vista desde el punto de vista de la estimación del trader.
El resultado también puede escribirse como:
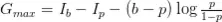
Expresión que representa una aproximación a la diferencia entre la información conocida por el trader y la conocida por el “mundo exterior”.
El resultado anterior puede resumirse en que el aumento de utilidad esperada óptimo es igual a la información previa conocida por (y de acuerdo con) el trader acerca del resultado de la operación menos la información previa conocida por el “mundo exterior” acerca de ese resultado, considerada desde el punto de vista del trader.
Dicho en términos más sencillos: el aumento de utilidad esperada dependerá de cuánta información adicional afirme tener el trader con respecto a la que se conoce en un mercado eficiente.
Saludos,
X-Trader