Los mercados financieros son, por naturaleza, dinámicos y cambiantes. Las condiciones actuales rara vez reflejan fielmente las del pasado lejano. El volumen negociado, los participantes del mercado e incluso los marcos regulatorios evolucionan con el tiempo, alterando las características de los activos. Este fenómeno plantea un problema fundamental para los traders: ¿cómo diseñar estrategias robustas si el pasado más lejano es irrelevante y el pasado más reciente no tiene suficientes datos?
La solución tradicional ha sido limitarse a analizar un período corto de datos históricos del pasado reciente, más representativo del probable futuro cercano. Sin embargo, esto conlleva otro desafío: la falta de significancia estadística. ¿Cómo podemos evaluar adecuadamente una estrategia si disponemos de tan pocos datos? Aquí es donde entra en juego una herramienta poco conocida o
utilizada: las series temporales sintéticas.
El Problema de las Series Temporales Sintéticas Clásicas
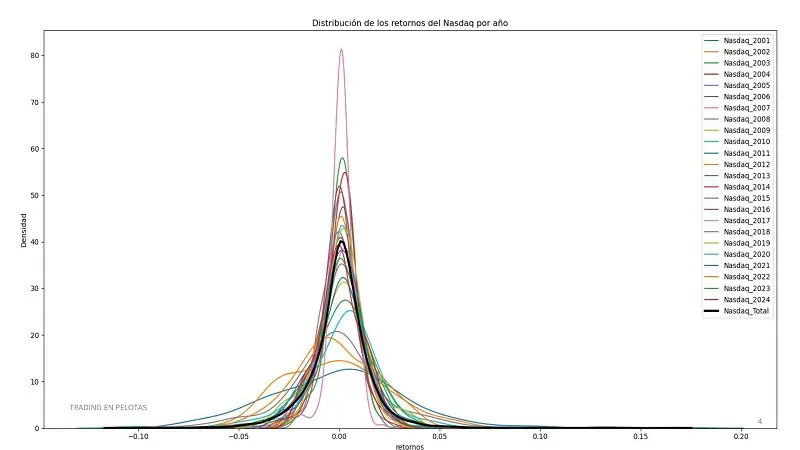
Generar series temporales sintéticas no es un concepto nuevo. Los métodos tradicionales suelen centrarse en replicar la distribución de retornos del activo original, pero esta aproximación tiene un defecto crítico: pierde la estructura inherente del precio. Por ejemplo, en una tendencia alcista, es común que las velas alcistas superen a las bajistas, y estas tiendan a agruparse en patrones específicos. Los métodos clásicos ignoran estas relaciones temporales, generando series que, aunque estadísticamente similares, no reflejan el comportamiento real del activo.
El resultado son simulaciones irrelevantes que pueden llevar a conclusiones erróneas sobre la validez de una estrategia. Si queremos diseñar sistemas verdaderamente robustos, necesitamos un enfoque que preserve tanto la distribución estadística como la estructura del precio.
Mi Metodología: Montecarlo por Bloques
Para resolver este problema, ideé un método (aunque seguro que no debo ser el único que utiliza algún sistema similar) que combina la variabilidad de las series sintéticas con la preservación de los patrones del activo original. El proceso consta de tres pasos principales:
1. División en Bloques y Sub-Bloques
La serie temporal original se divide en bloques de 30 velas, y cada bloque se subdivide en sub-bloques de 5 velas (equivalente a una semana en velas diarias). Esta estructura permite mantener las características locales del precio.
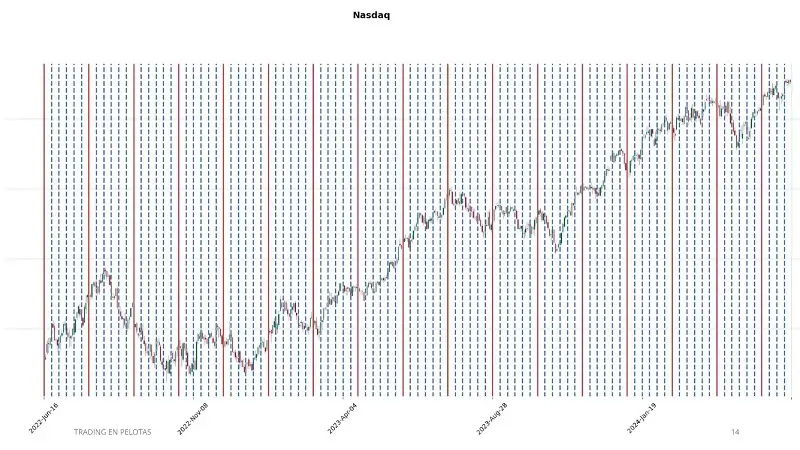
2. Mezcla Aleatoria de Sub-Bloques
Los sub-bloques se mezclan aleatoriamente dentro de cada bloque principal. Esto genera variabilidad en la serie sin perder los patrones locales.
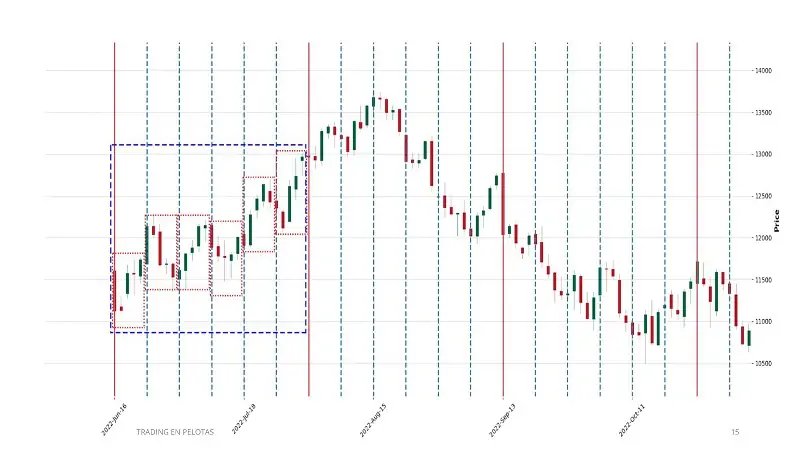
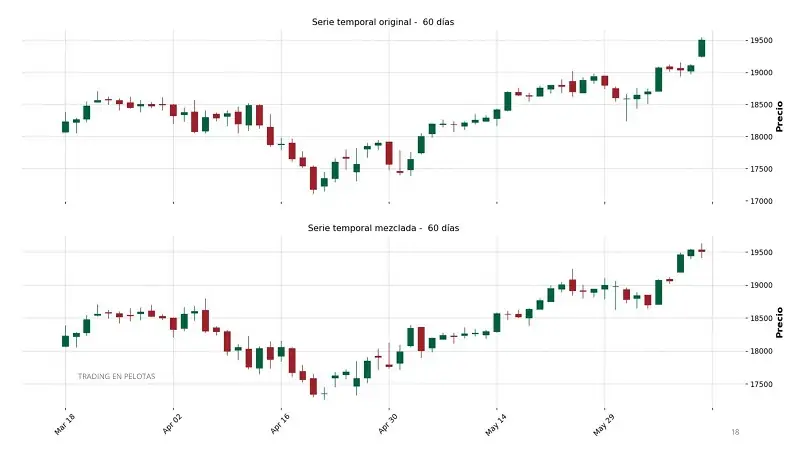
3. Reconstrucción de la Serie Temporal
Convertimos la serie original a retornos porcentuales antes de aplicar el método, asegurándonos de mantener las propiedades estadísticas globales. Luego, reconstruimos la serie temporal desde los retornos.
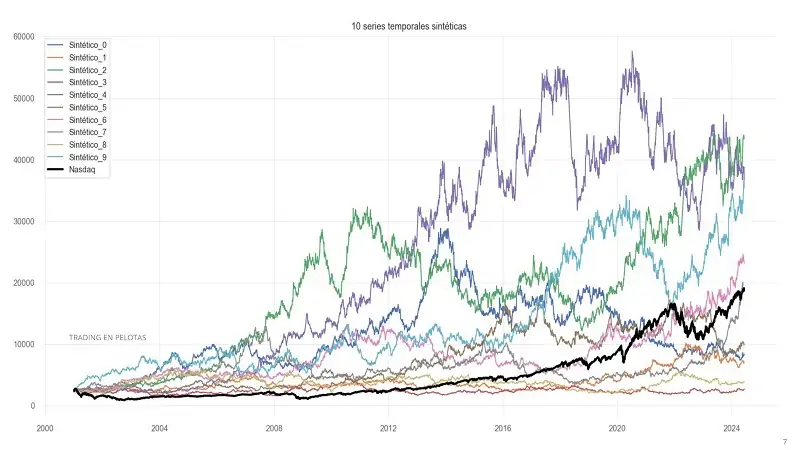
Este enfoque ofrece dos ventajas clave:
- Generación de miles o millones de series temporales con características similares al activo original.
- Conservación de la estructura del precio, lo que garantiza simulaciones más realistas.
Aplicación Práctica: Evaluación de Estrategias
La capacidad de generar múltiples series sintéticas abre nuevas posibilidades para evaluar estrategias de trading. En lugar de confiar únicamente en un backtest sobre la serie original, estas series nos permiten realizar miles de simulaciones y analizar el rendimiento en un amplio rango de escenarios.
Estrategia Sobreoptimizada
Consideremos una estrategia que aparentemente funciona bien en la serie original, alcanzando un Sharpe ratio elevado. Sin embargo, al someterla a pruebas con series temporales sintéticas, los resultados cuentan otra historia:
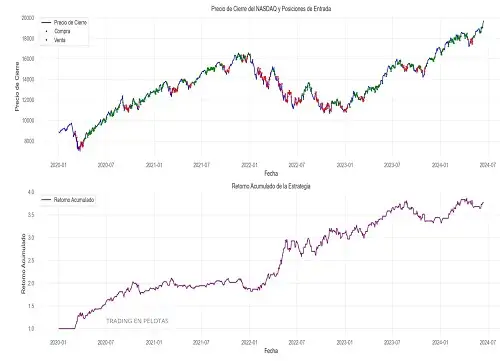
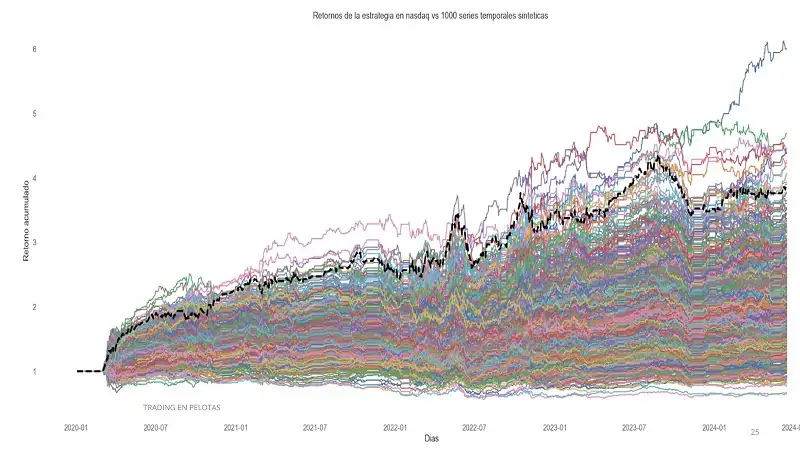
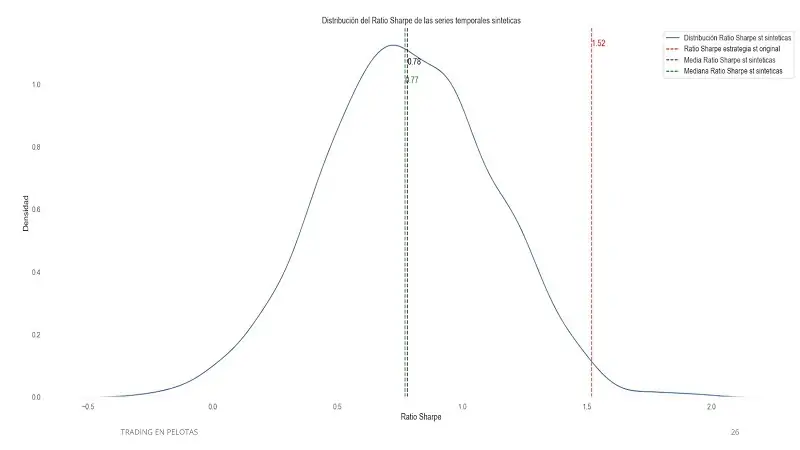
- La distribución del Sharpe ratio en las series sintéticas muestra una gran dispersión, con un rango que incluye valores negativos. Esto indica que la estrategia depende demasiado de las condiciones específicas del pasado reciente y no es capaz de adaptarse a escenarios diferentes.
- Los gráficos relacionados con esta estrategia muestran cómo, aunque pueda parecer prometedora en el backtest original, su desempeño es inconsistente en las simulaciones. Esto refuerza la idea de que los buenos resultados iniciales son un reflejo de sobreoptimización.
Estrategia Robusta
Por otro lado, una estrategia robusta se comporta de manera consistente tanto en la serie original como en las series sintéticas. Los gráficos de esta estrategia evidencian:
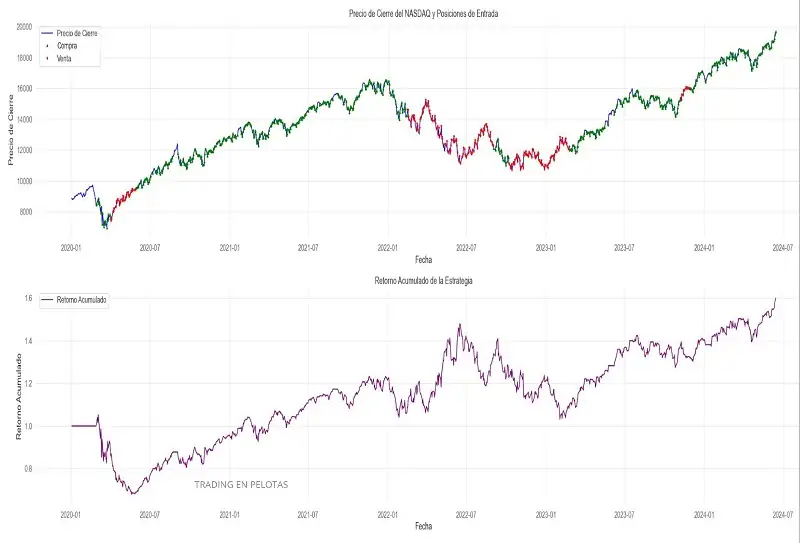
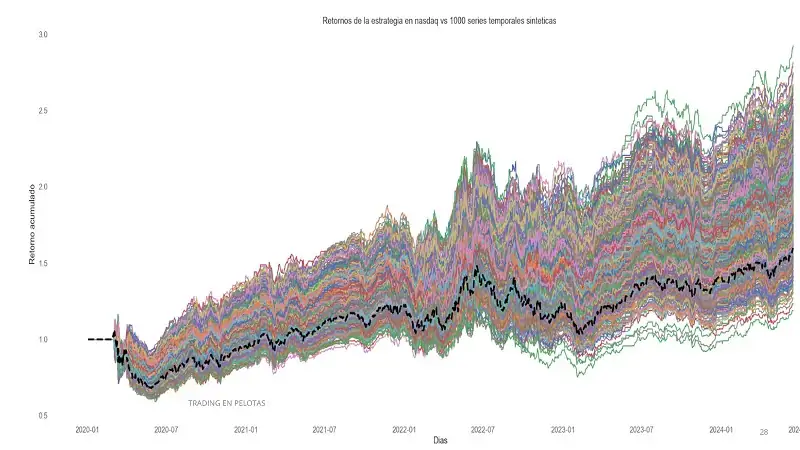
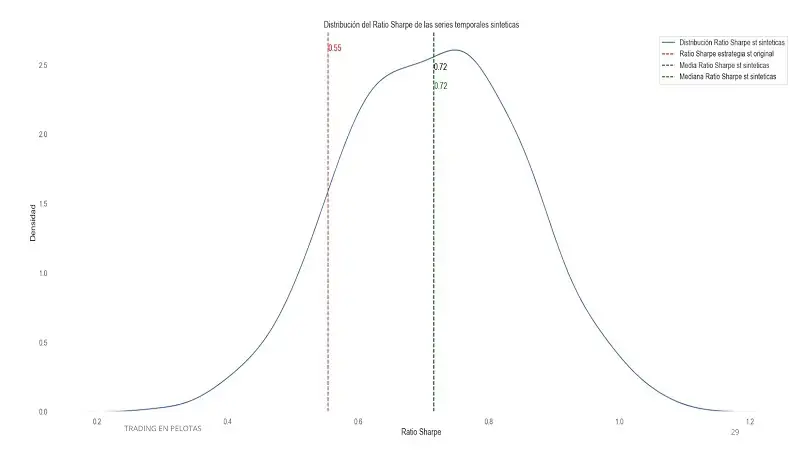
- Una distribución del Sharpe ratio más concentrada y con valores mayoritariamente positivos, lo que indica una menor dependencia de condiciones específicas.
- Esta robustez se traduce en confianza para implementar la estrategia en un entorno real, ya que ha demostrado su adaptabilidad en múltiples escenarios simulados.
Este análisis no solo valida el desempeño de una estrategia, sino que también permite ajustarla para alcanzar el percentil mínimo aceptable de Sharpe ratio, optimizando el equilibrio entre rendimiento y robustez.
Conclusión
Los mercados financieros son dinámicos y no estacionarios, lo que complica el diseño de estrategias adaptativas. Las series temporales sintéticas, especialmente cuando se generan mediante métodos avanzados como el Montecarlo por bloques, ofrecen una solución práctica y efectiva a este problema.
Esta metodología no solo resuelve la falta de datos históricos representativos, sino que también permite evaluar estrategias con un nivel de profundidad más elevado. En un mundo donde la adaptabilidad es clave, herramientas como esta pueden marcar la diferencia entre una estrategia promedio y una verdaderamente robusta.
Artículo publicado en el número 61 de la revista Hispatrading. Regístrate en Hispatrading.com de manera completamente gratuita para acceder a más artículos como este.