En esta serie, de dos artículos, estamos analizando el proceso de asignación de activos mediante criterios múltiples, empleando como hilo conductor un portfolio simulado con el que iremos detallando los pasos a seguir para su correcta optimización y rebalanceo en diferentes escenarios. Veamos la segunda y última parte.
Para calibrar la calidad de una optimización con alguno de los criterios mencionados es preciso comparar su performance con la de otra carrera sin optimizar que llamaremos portfolio benckmark. Existen dos enfoques sobre su construcción: Algunos gestores prefieren emplear como benckmark carteras equiponderadas por riesgo (Equal Risk Portfolio). Si bien el problema de este enfoque es que el riesgo de un activo -por ejemplo medido por la beta en el caso de las acciones de un índice- es un parámetro muy volátil y hay que hacer continuos ajustes. Por ello la mayoría de los gestores utilizan como benckmark portfolios tipo 1/n o equiponderados por valor (Equal Weighted Porfolios). Esta práctica está muy extendida en la industria; existen índices equiponderados y productos invertibles como ETFs1 que baten sistemáticamente a los índices convencionales.
Construir benckmarks de este tipo para carteras de acciones es muy sencillo, basta con asignar cantidades iguales y dividir por la cotización de cada valor para calcular el número de acciones de cada activo. En este caso la granularidad es máxima, incluso con cuentas poco capitalizadas. Sin embargo, al trabajar con portfolios de sistemas que operan con futuros la asignación en proporciones iguales será mucho más imprecisa.
Lo primero que tendremos que calcular es la unidad de asignación o capital requerido por contrato para cada vector de inversión:
Vi = G + DDm * n
Donde G son las garantías exigidas por el broker para cada producto y DDm es el drawdown máximo del sistema. Es conveniente tomar como referencia el DD obtenido en simulaciones de Montecarlo al 95% e incluir un factor de confianza n que expresa nuestro grado de certidumbre sobre el DDm. Este tipo de asignación, que denominaremos «Asignación Equiponderada por Simulación de Montecarlo» (AESM), incluye por tanto dos variables que habrá que considerar en los rebalanceos múltiples: G, cuyo valor puede aumentar o disminuir en el tiempo y DDm que solo puede aumentar.
Dado que entre los Vi que forman la cartera existe diferente grado de correlación, el DD combinado suele ser más bajo que el de la suma de los Vi. Por ello para determinar el capital necesario para operar la cartera se toma como referencia el drawdown de Montecarlo en el nivel de portfolio.
ESTUDIO DE CASO: OPTIMIZACIÓN DE UNA CARTERA SISTEMÁTICA CON OBJETIVOS MÚLTIPLES
Sea Sp un portfolio que combina las 8 siguientes estrategias intradiarias y tipo swing cada una de las cuales opera en un mercado distinto (ver Tabla 1):
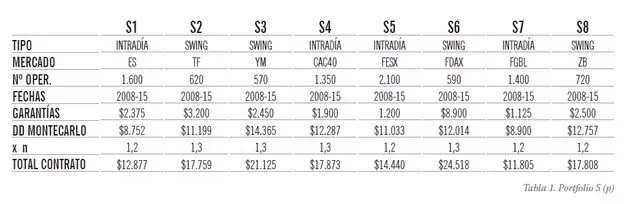
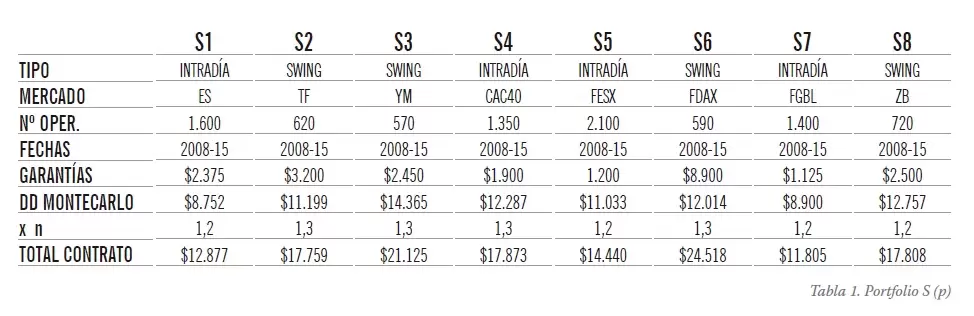
Partiendo de un capital de $300.000 y de las series históricas de las operaciones en base diaria del período: 2008-2015, vamos a construir cuatro carteras tipo que responden a los siguientes perfiles:
- Alta aversión al riesgo: Para lo que utilizamos el modelo de Mínima Varianza.
- Aversión media: Maximizamos el Ratio Omega.
- Alta diversificación: Para lo que optimizamos maximizando el Diversification Ratio (DR).
- Equilibrio entre retorno y DDm: Maximizamos el Ratio de Calmar.
El primer paso será construir la cartera alícuota o benckmark en la que el capital queda distribuido del siguiente modo:
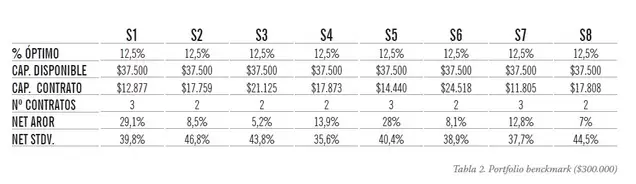
- Ponderación mínima: 3%
- Ponderación máxima: 40%
- Tolerancia de capital 2: ±10%
- Algoritmo evolutivo
- Tipo de búsqueda 3: Profunda.
El proceso de optimización es de período único y nos permite determinar si los criterios seleccionados satisfacen los objetivos del modelo y superan al portfolio benchmark en los ratios específicos que tratamos de maximizar para cada perfil inversor. También podemos comparar la eficacia de las carteras tipo generadas, pero en ningún caso debemos utilizar los resultados con carácter predictivo. El proceso de optimización es en sí mismo una evaluación in-sample y será necesario implementar una evaluación tipo walk-forward para comprobar que el vector de pesos asignados a los activos es consistente también en las regiones no optimizadas u out-sample. En la siguiente imagen podemos ver cada modelo de cartera en relación con la rentabilidad anualizada (µp) y Riesgo (σp) del benckmark (líneas punteadas):
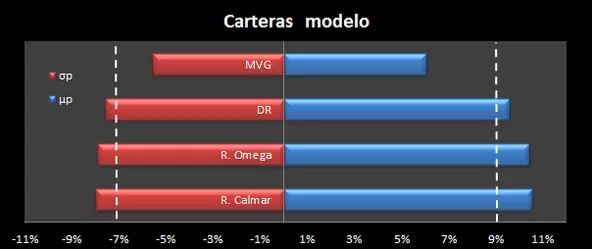
En la Tabla 3 se muestran las estadísticas generales de cada modelo:
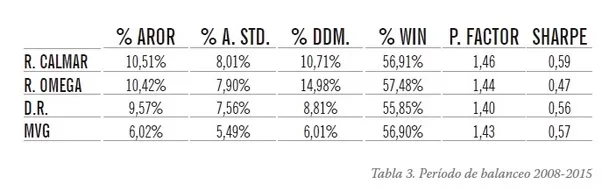
Con los ratios Calmar y Omega se obtienen rentabilidades muy similares (10,51% y 10,42%) para un nivel de riesgo similar. Sin embargo no se obtienen del mismo modo: La cartera Omega está mucho menos diversificada; la mayor parte del peso se concentra en tres activos mientras el resto tiene la ponderación mínima permitida (3%). En este escenario salta a la vista que para el gestor profesional resultará más atractiva la cartera Calmar que la Omega.
En los siguientes gráficos podemos ver los detalles del proceso de asignación y los pesos relativos de cada sistema en ambos portfolios:
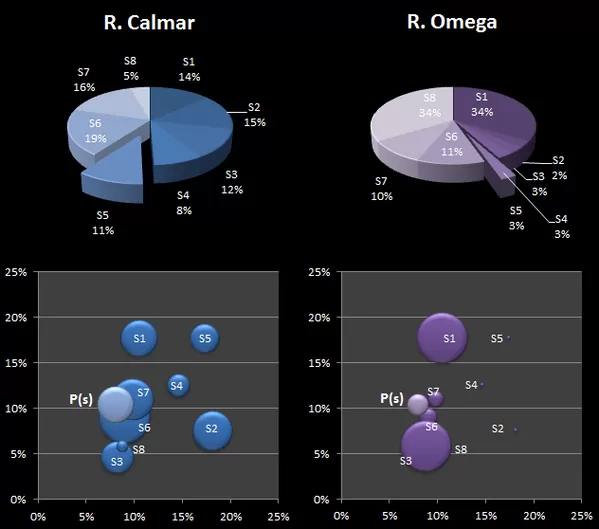
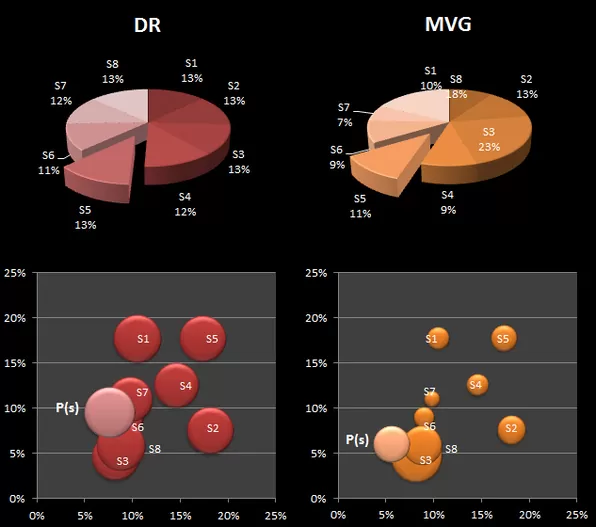
El portfolio de máxima diversificación (DR) parece cumplir su propósito relativamente bien en términos R/R al asignar porcentajes a los activos con los que se consigue una disminución efectiva del drawdown máximo (DDm), una rentabilidad aceptable y una diversificación mucho mejor que con los dos anteriores ratios. De hecho, con una asignación próxima a la de la cartera benckmark consigue unos ratios ligeramente mejores.
Por último, el portfolio de máxima varianza global (MVG) consigue disminuir eficazmente el riesgo de la cartera medido por la desviación anualizada. Eso sí, el AROR ya no es tan atractivo.
En general observamos que cada ratio diana satisface globalmente el modelo de cartera para el que fue propuesto. Ahora bien, ¿podemos elegir uno que sea objetivamente mejor? Esta pregunta no tiene fácil respuesta. De hecho los términos «mejor» y «peor» dependen del tipo de cartera que queremos construir.
REBALANCEO DEL PORTFOLIO Y WALK-FORWARD
Como ya hemos visto, las ponderaciones óptimas de una cartera van deteriorándose con el tiempo. Los activos pueden concentrar más riesgo, variar su correlación con otros activos o requerir una porción de mayor/menor de capital. Por tanto, para garantizar que la composición de la cartera se mantiene alineada con los con los objetivos del modelo y con los intereses de los inversores se hace necesario implementar una política de rebalanceos periódicos.
Existen diferentes métodos de rebalanceo (Carmichael4, Jaconetti y Kinniry5) que podemos agrupar en tres categorías:
1. Calendar Rebalancing
Rebalanceo periódico basado en intervalos temporales fijos (meses, trimestres, años). Este es el método más común y cuando se compara con otras estrategias dinámicas más sofisticadas casi siempre sale muy bien parado. El intervalo de rebalanceo estándar en los gestores de fondos tradicionales (renta variable y mixta) es el anual. Sin embargo, en programas inversores más agresivos también suele ser común el rebalanceo trimestral y mensual. La frecuencia del rebalanceo depende de factores como:
- Los gastos de transacción.
- La duración media de las operaciones.
- Las salidas y entradas de capital al fondo o programa inversor.
- El ciclo del mercado (mayor/menor volatilidad).
- La evolución de la propia cartera.
2. Volatility-Based Rebalancing
Este método de rebalanceo se implementa cuando se desean mantener estables los pesos de los tipos o grupos de activos que forman parte de la cartera. De este modo, si la política de un fondo es mantener siempre una proporción: 20% RF, 40% RV nacional y 40 RV internacional se establece, por ejemplo, una banda de fluctuación del ±5% y cuando alguno de los grupos la rebasa se rebalancea la cartera.
3. Risk-Based Rebalancing
En muchos casos (política del fondo, requisitos regulatorios) los gestores se ven obligados a no rebasar cierto nivel de riesgo permitido. De este modo rebalancean periódicamente los activos con el fin de reducir la exposición o desapalancarse cuando el porfolio se aproxima al umbral establecido. En este grupo estarían los VaR-based portfolios; cuando el valor en riesgo rebasa el nivel marcado por el estimador de confianza se procede a reajustar la cartera.
Por otra parte, el rebalanceo en el tiempo de un portfolio puede hacerse siguiendo el esquema de período único (no se reinvierte el beneficio) o de periodos múltiples (reinversión continua). En el primer caso se realiza la asignación de capital distribuyendo entre los diferentes vectores una cantidad fija en cada período. En el segundo, el gestor tiene más flexibilidad al poder redistribuir el beneficio entre los vectores disponibles incrementando su tamaño o incorporar progresivamente nuevos vectores.
Con el portfolio sistemático descrito en el apartado anterior vamos a realizar un ejemplo de rebalanceo por períodos anuales. Utilizaremos el modelo de período múltiple, balanceando en cada corte anual el capital disponible al término del período anterior. El criterio diana será el ratio de Calmar.
Para que la simulación resulte más realista, utilizaremos el siguiente esquema walk-forward en el período 2008-2015:
- Balanceamos la cartera con el capital inicial disponible hasta el 31 del 12 de 2008 y aplicamos los pesos asignados a cada vector al año 2009.
- El último día hábil de 2009 se hace un nuevo balanceo con el capital disponible en esa fecha (capital inicial ± beneficio en 2008) y obtenemos los porcentajes de asignación y número de contratos con los que se empezará a operar el portfolio en 2010.
- (…) El proceso continúa así hasta 2015.
- La serie resultante 2009-2015 será el Out-Sample del portfolio.
- No se han aplicado gastos. El modelo supone que entramos a operación cerrada. Es decir, esperamos a que cada sistema esté flat antes de incrementar o disminuir su peso en la cartera.
En la imagen inferior tenemos el gráfico de pesos de los sistemas por períodos balanceados con el ratio Calmar y la evolución del número total de contratos en ambas series:
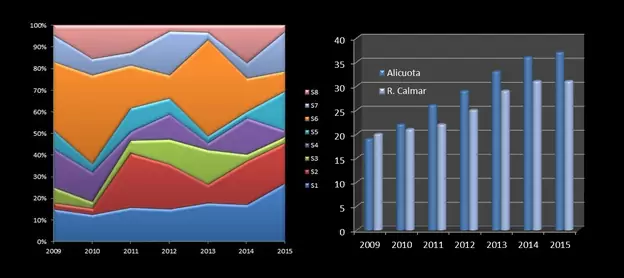
Como podemos ver, en determinados periodos algunos sistemas llegan al valor mínimo de asignación que es del 3%. Es muy recomendable balancear la cartera estableciendo un máximo y un mínimo para cada activo. De lo contrario, encontraríamos periodos bien con sistemas inactivos, bien con una excesiva concentración de capital. Y esto, además de ser inaceptable en la práctica, contravendría el principio central de toda teoría de carteras que es la diversificación como mecanismo para diluir el riesgo.
Seguidamente mostramos equity curve del portfolio benchmark (en azul) y del portfolio balanceado con el ratio Calmar (línea roja):
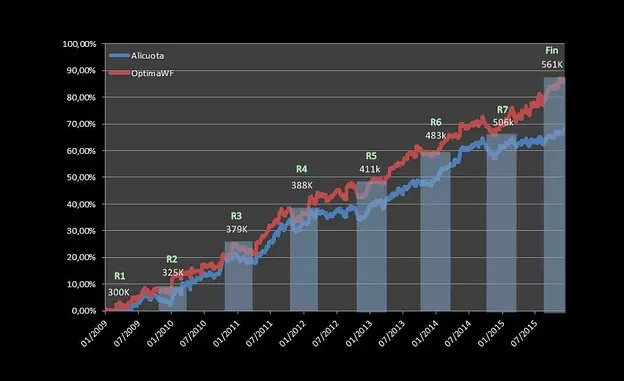
En cada corte temporal (R1…R7) hemos incluido la nueva cantidad a balancear al inicio de cada período. Con sistemas intradiarios o tipo swing de alta cadencia podríamos haber elegido un modelo de rebalanceo mucho más agresivo, con cortes trimestrales e incluso mensuales. En cualquier caso, bástenos lo expuesto hasta aquí como ejemplo ya que la dinámica a seguir es la misma.
Otra opción interesante podría ser combinar la asignación de período único con estrategias de gestión monetaria (MM) que optimicen de manera continua el tamaño de la posición, eligiendo para ello fórmulas consecuentes con los objetivos generales del portfolio o programa inversor. De este modo estaríamos combinando un enfoque estratégico y a largo plazo, centrado en los objetivos de construcción con un enfoque táctico o de operativa.
Lógicamente antes de implementar el portfolio debemos realizar una evaluación exhaustiva incluyendo simulaciones de Montecarlo, análisis de riesgos o de escenarios adversos6, elaboración del test Profile y determinación del capital mínimo para operar la cartera, pero eso ya lo dejaremos para futuras entregas.
Acerca del autor
Andrés A. García es Doctor en Filosofía, especializado en Lógica y Filosofía de la Ciencia, Doctor en Ciencias de la Educación y Experto en Nuevas Tecnologías. Durante más de 20 años ha compaginado la enseñanza y la operativa por cuenta propia, centrándose en la última década en el desarrollo de algoritmos automáticos de trading en los mercados de futuros estadounidenses y europeos. Es propietario de una de las páginas web más conocidas y visitadas en España sobre trading de sistemas y temas afines: TradingSys.org. También es autor de un libro sobre “Futuros de renta fija y operativa intradiaria” (2009), de numerosos artículos sobre mercados financieros en diversas webs y publicaciones especializadas y ha impartido conferencias en varias universidades. Actualmente es profesor del curso de postgrado «Sistemas y modelos cuantitativos de trading algorítmico» organizado por la Universidad Politécnica de Madrid. Desde 2010 es cofundador y socio de la empresa Optimal Quant Management, que ofrece formación online avanzada y de alta calidad sobre trading de sistemas. Así mismo es socio y cofundador de la empresa ATP Capital Management LLC (2013), un CTA (Commodity Trading Advisor) que opera en EEUU.
Referencias
1 Uno de los más populares es el Guggenheim S&P 500 Equal Weight (RSP).
2 Debido a la baja granularidad de los futuros se permite un redondeo del capital necesario por contrato. Con esto evitamos que los algoritmos nos den soluciones subóptimas cuando el capital disponible está en el entorno del capital exigido.
3 Tiempo por escenario limitado a 120 s.
4 Carmichael, I. (2009), «Rebalancing a Comparison of Methods»: https://citeseerx.ist.psu.edu/doc_view/pid/b1e8550930344ff8b08ea438401ee84a8000f967
5 Jaconetti C., Kinniry F. y Zilbering, Y. (2010), «Best Practices for Portfolio Rebalancing», Vanguard Research. https://indexacapital.com/bundles/unaiadvisor/docs/papers/2010-Vanguard-Best-practices-for-portfolio-rebalancing.pdf?v=102
6 Por ejemplo, mediante las técnicas del VaR y CVaR comentadas en otro artículo publicado en Hispatrading: Nuevas métricas del riesgo y sus aplicaciones en portfolios de sistemas Parte 1.
Artículo publicado en el número 30 de 2017 de la revista Hispatrading. Regístrate en www.hispatrading.com de manera completamente gratuita para acceder a más artículos como este.