Optimización y Rebalanceo de Portfolios Sistemáticos I

Tras unas pinceladas históricas sobre las dos formas paradigmáticas de entender la Teoría de Carteras, nos adentraremos en la optimización de portfolios construidos con productos no convencionales, como los sistemas de trading con derivados. En esta serie, de dos artículos, analizaremos el proceso de asignación de activos mediante criterios múltiples, empleando como hilo conductor un portfolio simulado con el que iremos detallando los pasos a seguir para su correcta optimización y rebalanceo en diferentes escenarios.

LOS DOS ENFOQUES PARADIGMÁTICOS DE LA TEORÍA DE CARTERAS

La “Moderna Teoría de Carteras” representa un importante avance respecto a los modelos tradicionales de asignación de activos, en su mayoría subjetivos y ambiguos. Es la primera vez que se aplican con éxito las matemáticas financieras a un problema de toma de decisiones tan escurridizo y complejo como la construcción y optimización de carteras. Pero han pasado ya seis décadas desde su formulación y, al perecer, muchos gestores tradicionales y de Hedge Funds¹ siguen aferrados al enfoque media-varianza (M-V) formulado por Markowitz² en 1952. Este modelo de asignación proporciona un marco conceptual sólido para balancear  carteras que combinan acciones y bonos, pero resulta bastante inapropiado para bregar con productos complejos que invierten en decenas de mercados internacionales, realizan sofisticadas operaciones de cobertura con derivados e incluso incorporan programas de trading algorítmico. Y es que el modelo M-V y sus diversas variantes³ solo es útil para inversores que tienen “preferencias cuadráticas”; es decir, cuyo perfil de aversión puede situarse linealmente en algún punto de una Frontera Eficiente definida en términos de retorno por unidad de riesgo.

Diferentes estudios se han encargado en poner de manifiesto que no existe una percepción unívoca del riesgo. Por tanto, más que un “criterio de utilidad”, iríamos a una multiplicidad de criterios, lo que implica emplear diferentes estimadores del riesgo en diferentes contextos de inversión^4,5.

Por otra parte, el bello esquema de maximizar el retorno esperado para cada nivel de riesgo o, a la inversa, minimizar el riesgo (medido en términos de desviación estándar) para cada nivel de retorno esperado (en términos de rentabilidad media), cuando se lleva a la práctica choca contra el infranqueable muro de la incertidumbre:

• Es muy difícil proyectar el beneficio a futuro empleando series históricas. De hecho, como pusieron de manifiesto estudios académicos posteriores^6,7 la determinación del retorno medio es un factor mucho más crítico en el modelo M-V que la covarianza entre activos. Los errores de estimación de la media son hasta 20 veces más importantes que los errores en la desviación.
• La normalidad del retorno es otro de los elementos que suscitan gran controversia. Este supuesto del modelo M-V, que procede de la hipótesis del Random walk  o Teoría Eficiente de los mercados, se asienta en la idea de que los precios de los activos siguen un paseo aleatorio en el tiempo, por lo que su beneficio medio (en días, semanas o meses) está normalmente distribuido. Ahora bien, se ha demostrado que muchos activos se mueven en rachas o tendencias de gran amplitud que generan largas colas en la distribución del retorno, apartándose tres desviaciones o más de la media.
• Aunque la correlación entre activos se ha mostrado más estable y predecible que el retorno, también genera un problema práctico, sobre todo en carteras de gran tamaño: el cómputo de los porcentajes de asignación a partir de una inmensa matriz de varianzas y covarianzas es complicado y arroja resultados cada vez más imprecisos a medida que aumenta el tamaño. Con todo existen algunas simplificaciones como la propuesta por Sharpe en 1963. También existen optimizadores cuadráticos para el cómputo M-V a gran escala⁸.  

No me extenderé más con este asunto. Bástenos señalar que, pese a sus deficiencias, el modelo M-V ha contado -y en buena medida aún cuenta- con el favor del mundo académico y de la industria financiera. Proporciona un marco intuitivo y coherente para tomar decisiones de inversión y balancear portfolios sencillos. Sin embargo, cuando nos adentramos en la gestión alternativa y la construcción de carteras que incorporan productos derivados y sistemas de trading cuantitativo, se hace preciso buscar nuevas metodologías y herramientas.

Un planteamiento diferente, nacido también en la década de los 50, busca aumentar el capital a la mayor tasa de crecimiento posible, o lo que es lo mismo, maximizar la media geométrica del retorno de la cartera.  De este modo, la función de utilidad renuncia a balancear el riesgo y asume que un “inversor racional” elegirá la combinación de activos con la que obtenga el valor más alto de la riqueza terminal . Por simplificar, podemos situar el origen de este segundo enfoque en John Kelly (1956) y su determinación, en juegos de azar, de la fracción óptima a apostar para maximizar el beneficio esperado. Descubrió que existe una proporción óptima de capital que el jugador puede arriesgar en cada apuesta (lo que de aquí en adelante se conocerá como Criterio de Kelly): conociendo la esperanza matemática (TA) del juego y el ratio entre apuestas ganadoras y perdedoras (WL), podemos determinar la facción óptima a arriesga como: F = TA/WL. Si el juego se compone de una secuencia n de apuestas ese valor de “f” será el que maximice la media geométrica de las apuestas y, en consecuencia, el que nos garantice en mayor retorno esperado. Este planteamiento posteriormente sería adapta-do por por Ralph Vince¹⁰ al caso del trading y la especulación bursátil.

Al margen del juego y la especulación, primero Latane¹¹ y luego otros autores como Breiman¹² o  Hakansson¹³ adaptaron la maximización de la media geométrica (GMM) al caso de la optimización y balanceo de carteras de acciones. Latane llegó a la conclusión de que la maximización de la media geométrica es un criterio de utilidad perfectamente válido para un inversor racional, ya que estaría maximizando la probabilidad de que en un horizonte terminal su cartera obtenga la máxima rentabilidad entre todas las combinaciones posibles de un conjunto dado de activos. Una vez establecida formalmente esta propiedad de los portfolios GMM, diversos autores han tratado de estimar el tiempo que se necesita para estar “razonablemente” seguros de que el modelo GMM bate a cualquier otro modelo de cartera¹⁴. Estudios posteriores  buscaron soluciones de compromiso entre los modelos M-V y GMM y también se  desarrollaron interesantes propuestas¹⁵ para determinar la Frontera Eficiente en portfolios tipo GMM.  

Es bastante conocida la controversia que surgió en el mundo académico entre ambos enfo-ques, pero visto en retrospectiva tampoco fue para tanto. Paul Samuelson¹⁶ fue el más crítico al aducir que no es lo mismo para un “inversor racional” maximizar el retorno que maximizar la función de utilidad. Y, efectivamente, balancear el retorno en función de la aversión al riesgo o, lo que es lo mismo, elegir el punto de la Frontera Eficiente que se co-rresponda con las preferencias de cada inversor tipo parece la opción más coherente. Pero claro, ese planteamiento solo es compatible con intereses cuadráticos y con un modelo M-V de periodo único. Si el inversor, como señaló incluso el propio Markowitz¹⁷, contempla períodos indefinidamente largos y la reinversión del retorno mediante rebalanceos periódicos, la opción mejor es el modelo GMM. Con todo, también reclamó prudencia al recomendar no seleccionar portfolios con media aritmética y varianza iguales o superiores a los obtenidos maximizando la media geométrica. A la obsesión por maximizar la función de utilidad como elemento central de la Teoría de Carteras, ya había respondido una década antes A. Roy¹⁸ con las siguientes palabras el mismo año que Markowitz dio a conocer su modelo:

“Al llamar a una función de utilidad en nuestra ayuda, se logra una apariencia de generalidad a costa de una pérdida de significación práctica y de aplicabilidad en nuestros resultados. Un hombre que busca consejos sobre sus acciones no estará agradecido por la sugerencia de que debe maximizar la utilidad esperada.»

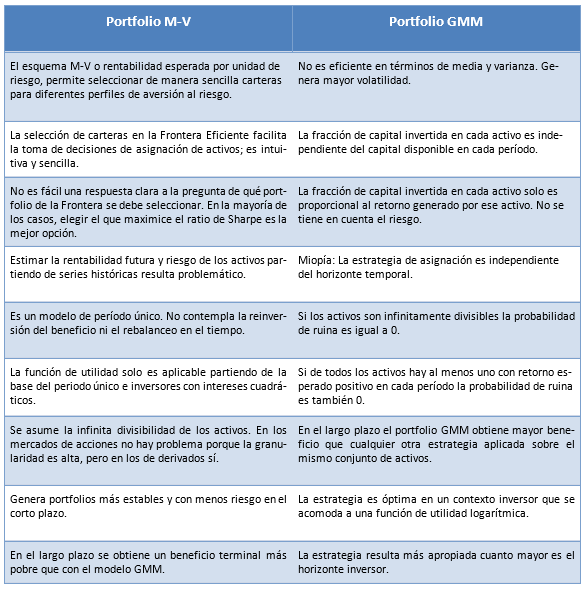
J. Estrada¹⁹ denomina con gran acierto “Portfolio S” o SRM²⁰ al tipo de cartera que se puede obtener balanceando conforme al modelo M-V y “Portfolio G” o GMM²¹ a aquella combinación de activos que maximiza la media geométrica. Seguidamente, y combinando los planteamientos de diversos autores, vamos a resumir en una tabla las ventajas y desventajas de cada modelo de cartera:

OPTIMIZACIÓN DE PORTFOLIOS DE SISTEMAS

Un portfolio o programa sistemático es una estructura de inversión que combina estrategias cuantitativas de trading aplicadas a diferentes tipos de activos (acciones, ETFs, futuros, opciones, etc.) Llamamos vector de inversión (Vi) al binomio sistema/activo. Cada Vi tienen un histórico de operaciones del que extraemos las estadísticas básicas igual que si se tratase de un producto cotizado y que utilizamos para balancear la cartera. Por tanto, desde la Teoría de Carteras, no hay diferencia entre balancear un portfolio de sistemas o de cualquier otra clase de activos. Sin embargo, cuando los sistemas se aplican a productos derivados hay que tener en cuenta dos características inherentes a estos productos: el apalancamiento y la granularidad. Trabajar con estructuras apalancadas implica asumir niveles de riesgo más altos por unidad de capital invertida y, la menor granularidad, impide una asignación tan precisa como en el caso de las acciones. El efecto de la escasa granularidad es más palpable en programas poco capitalizados.

Un modelo de optimización típico respondería al siguiente esquema:

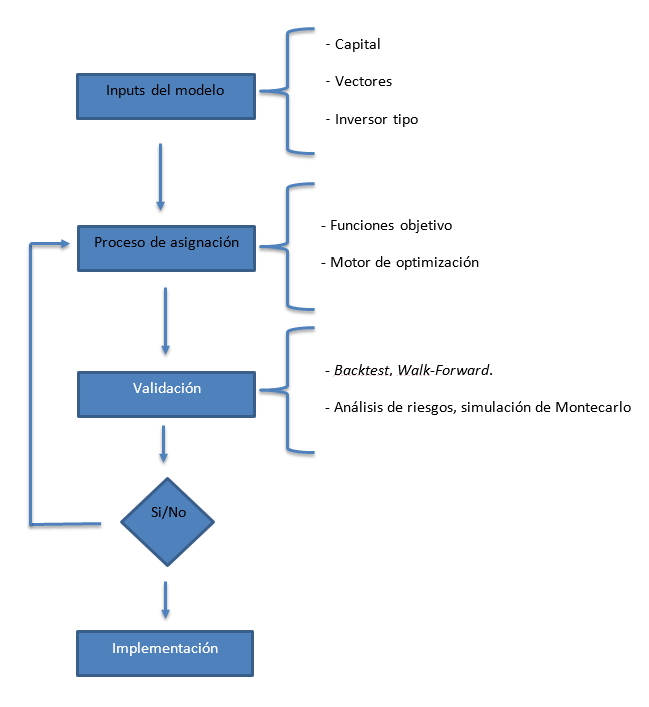
Los inputs del modelo son los condicionantes que determinan a priori el tipo de cartera que se puede construir. Las limitaciones de capital afectarán al tipo de sistemas y activos con los que se podrá trabajar. Esto es aún más crítico en la operativa con futuros. Cada vector de inversión requiere un capital  que estará determinado por las garantías exigidas para operar ese producto y por el drawdown (DD) del sistema. En este contexto entendemos por “granularidad” la unidad de asignación para cada vector o capital mínimo para operarlo con un con-trato. Cuando el portfolio es poco granular resultará muy difícil lograr un nivel de diversificación satisfactorio y un proceso de asignación eficiente con capitales pequeños.

Las estrategias a implementar dependerán de factores como las tecnologías disponibles, las características de los mercados en los que se va a operar y el enfoque estratégico del propio gestor. En la gestión profesional los vectores posibles también se ven afectados por cuestiones regulatorias específicas de cada producto como el apalancamiento permitido, la posible prohibición de posiciones cortas, el uso de determinado tipo de órdenes o las limitaciones sobre operativa con derivados.

Por otra parte, toda cartera se construye para satisfacer las demandas de un determinado perfil inversor. Cada perfil se caracteriza por un nivel de aversión al riesgo, una expectativa de beneficio y un horizonte de la inversión. Teniendo en cuenta estos condicionantes se cons-truye una cartera o programa modelo que satisface las demandas de un grupo específico de inversores. Cada vector de esa cartera podrá tener un riesgo superior o inferior siempre y cuando no se sobrepase el riesgo global especificado para el conjunto. Esto afecta de manera significativa al proceso de asignación y obliga a establecer restricciones en la ponderación máxima y mínima tanto en grupos de activo como en activos o vectores individuales. 

PROCESO DE ASIGNACIÓN

El proceso de asignación es la estrategia de ponderación diseñada para optimizar el beneficio y diluir el riesgo, diversificando el capital en diferentes proporciones entre todos los vectores disponibles.

En carteras medianas y grandes es un proceso complejo que requiere la utilización de software específico. Actualmente hay dos tendencias:

1. Aplicaciones propietarias. Son programas de optimización de carteras desarrollados por empresas para uso particular o corporativo. La diversidad es enorme: desde aplicaciones centradas en un modelo de asignación específico que trazan la Frontera Eficiente y poco más, hasta sofisticadas herramientas que permiten balancear un número ilimitado de productos, incorporar todo tipo de restricciones y aplicar criterios múltiples. Algunas permiten también rebalanceos periódicos,  análisis de riesgos y proyección a futuro del retorno esperado. Ejemplos de este grupo serían Optifolio y Morningstar Direct. 
2. Plataformas abiertas de programación y análisis estadístico. En el ámbito de la investigación destacan dos plataformas que se han convertido en un standard para el mundo académico: MATLAB y R. Del primero destacamos el complemento Portfolio Optimization que incorpora un completo conjunto de herramientas para el balanceo de carteras, análisis de riesgos, motores de optimización para el cálculo de la Frontera Eficiente según el modelo M-V y el CVaR, determinación de objetivos múltiples y rebalanceo. Pero sin duda, la mayor diversidad de aplicaciones para optimización de portfolios la encontramos en el entorno R que, al tener una estructura de código abierto y distribuirse bajo licencia GNU GPL, está ampliamente extendido en el mundo académico. Por su calidad y pertinencia para este artículo destacamos los siguientes proyectos:

– PortfolioAnalytics. Es un paquete de utilidades para la optimización de portfolios que incluye varios procedimientos de asignación y rebalanceo de activos. Se pueden realizar optimizaciones complejas; objetivos y escenarios, restricciones de todo tipo y análisis de riesgos.

– PerformanceAnalytics. Este paquete contiene una amplia colección de fun-ciones para el análisis de la rentabilidad y el riesgo en todo tipo de portfolios. Incluye funciones avanzadas para analizar retornos que no están distribuidos normalmente y numerosos ratios econométricos.

– fPortfolio. Completísima colección de funciones para optimizar carteras y realizar diversos tipos de backtests. Calcula y grafica la Frontera Eficiente por diferentes métodos e incluye otros modelos de asignación.

– FRAPO. Paquete de funciones de optimización y análisis de portfolios con-tenidos en el libro de Bernhard Pfaff²².

– ROML.  Entorno para la resolución de problemas avanzados de optimiza-ción de portfolios. Su principal aportación es que incluye un lenguaje algebraico de optimización.

– PortfolioEffectHFT. Paquete específicamente construido para el mundo HFT. Permite realizar asignaciones dinámicas y rebalanceos continuos en períodos intradiarios. Incluye herramientas para el auto calibrado del ruido en time frames muy pequeños y la monitorización del riesgo en tiempo real.

Un elemento clave en los procesos de asignación y rebalanceo es el motor de optimización. No todos los optimizadores sirven para resolver problemas de optimización de carteras. El uso de optimizadores genéricos consume mucho tiempo con problemas complejos en los que intervienen demasiados parámetros y objetivos múltiples. A menudo se obtienen resultados poco realistas o erróneos debido al uso de un método de optimización inadecuado. Los problemas de optimización de carteras requieren alguno de estos métodos de optimización: Cuadrático, lineal o vectorial, no lineal (tipo GNR), estocástico o evolutivo y generador aleatorio de carteras.

Por ejemplo, los problemas de asignación con el modelo M-V y la determinación de  la Frontera Eficiente requieren un optimizador cuadrático, si utilizamos como función objetivo el CVaR o el Ratio Rachev será más eficiente una optimización lineal y si  optimizamos con el ratio Omega será preciso utilizar un optimizador estocástico o evolutivo. Muchos de estos problemas y otros que no caen en estos grupos pueden resolverse por el procedimiento de los “portfolios aleatorios”²³. Básicamente se trata de generar permutaciones aleatorias de los porcentajes de asignación que satisfagan las restricciones del modelo. El conjunto resultante de carteras puede estar formado por miles o cientos de miles de portfolios alternativos y daría lugar a gráficos como estos:

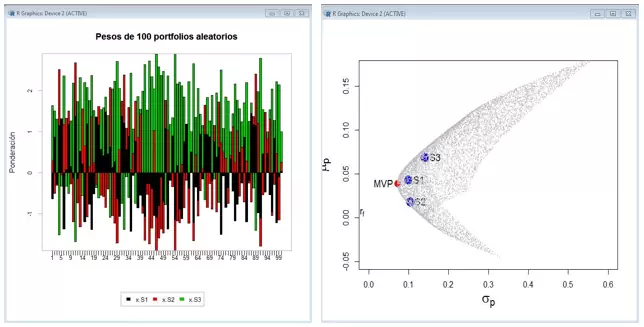
La principal ventaja de esta técnica es que permite rastrear todas las carteras posibles en el espacio de búsqueda de un problema de optimización específico y no solo el subconjunto de carteras situado en la Frontera Eficiente o aquella única combinación de activos que maximiza el criterio diana elegido.

CRITERIOS DIANA O FUNCIONES OBJETIVO

Capítulo aparte merece el análisis de los distintos criterios de optimización. Cada criterio o función objetivo debe ser consecuente con los inputs del modelo o planteamientos generales a los que responde la construcción del portfolio. Por ejemplo, para un inversor tipo con intereses cuadráticos y que quiera maximizar la función de utilidad del modelo M-V, el criterio para balancear la cartera será el ratio de Sharpe. Para otro con menor aversión al riesgo, un horizonte temporal mayor y que no quiera reinvertir el beneficio utilizaremos un ratio que priorice el retorno (como el Omega) y un enfoque de período único. Si el inversor es aún más agresivo y busca componer muy deprisa reinvirtiendo el beneficio en un horizonte temporal indefinido nos iríamos al MMG multiperíodo con política de rebalanceos trimestral o mensual.

En este punto conviene aclarar un concepto: un enfoque multiperíodo implica que el beneficio se reinvierte a perpetuidad y que los rebalanceos se hacen con el capital generado al final cada periodo. Por el contrario, en un enfoque de período único el inversor hace retiradas periódicas o el fondo reparte el beneficio obtenido como dividendo. Se hacen balanceos para mantener el portfolio alineado con los objetivos iniciales del programa (por ej. en términos de riesgo o diversificación), pero no con el propósito de componer el retorno.

Veamos pues los principales criterios a utilizar:

a) Optimización M-V

Siendo el Retorno Esperado (µ_p), la varianza (σ²_p) y el activo libre de riesgo (R_f) el problema de optimización consistiría, como hemos visto, en maximizar el ratio de Sharpe (SR_p), de tal modo que:

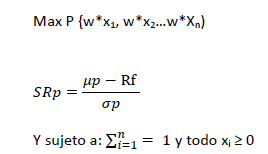
También se puede obtener un portfolio eficiente minimizando la varianza  (σ²_p) para un nivel de retorno esperado (o a la inversa):

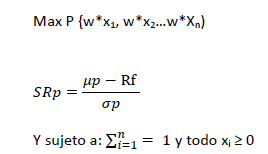
b) Optimización GMM

Para optimizar la media geométrica partiendo de la media aritmética (µ_p)  y la varianza (σ²_p) de las rentabilidades empíricas en series históricas podemos emplear la siguiente expresión logarítmica:

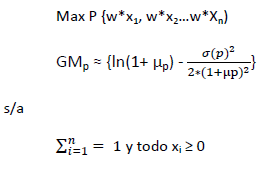
Bernstein y Wilkinson²⁴ proponen la siguiente fórmula simplificada para la media geométrica, aunque es una aproximación con resultados más imprecisos:

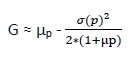
c) Optimización MVG (Mínima Varianza Global)

La cartera MVG es la que presenta la varianza mínima posible, con independencia der retorno esperado. Esto implica resolver el siguiente problema de optimización:

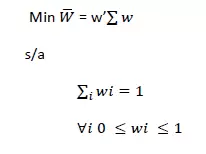
Siendo W el vector de los pesos asignados a cada activo y ∑ la matriz de covarianzas.

d) Optimización DR (Diversification Ratio)

En este modelo establecemos como criterio de asignación la máxima diversificación global de la cartera. Para ello seguimos el enfoque de Yves Choueifaty²⁵ que propone el Diversification Ratio (DR) como estimador que mide la volatilidad media ponderada por tamaño frente a la volatilidad general de la cartera.

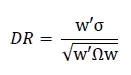
Siendo w la matriz de ponderaciones, σ el vector de volatilidades y w’Ωw el producto de la matriz de covarianzas y ponderaciones.

Por tanto, el problema de optimización es:

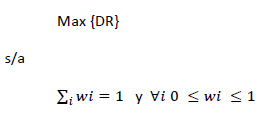
e) Optimización del riesgo máximo en términos de VaR y CVaR

En general minimizar cualquier función del riesgo F(r) de un portfolio es un problema de optimización con la siguiente   estructura:

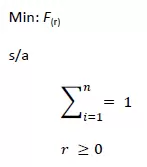
El VaR (valor en riesgo) y el CVaR (valor en riesgo condicional) son dos de los estimadores del riesgo más empelados por las instituciones financieras. El VaR puede definirse como la pérdida más alta que puede ocurrir con un determinado nivel de confianza. Por ejemplo, si VaR = 500€ y el intervalo de confianza es del 0,95, entonces tenemos una probabilidad del 95% de no exceder una pérdida de 500€ en el período al que hace referencia el VaR (datos diarios, semanales, mensuales, etc.)

De este modo la expresión a minimizar sería:

VaR = min {r ∈ R : P(-R > r) ≤ 1-α}

Siendo α el intervalo de confianza, R el retorno de la cartera y -R la pérdida.

En la práctica, a partir de la serie del retorno el VaR es el valor situado en el percentil α de la serie: 

VaR_α = Percentil (α, R)

Para una distribución normal del retorno, el CVaR²⁶ podemos definirlo como:

CVaR_α  = [-R | R ≤ -VaR_α], donde R ∈ (µ_p, σ²_p)

O lo que es lo mismo, la media ponderada de los valores situados en la cola derecha de la distribución a partir del valor de percentil (α, R).

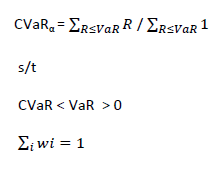
f) Optimización del ratio de Rachev²⁶

Es una medida tipo R/R en la que se compara la cola derecha de la distribución del retorno (Expected Tail Return) con la cola izquierda (Expected Tail Loss) en un intervalo de confianza similar al del VAR (0.05 < α > 0.95). Por tanto la expresión a maximizar sería:

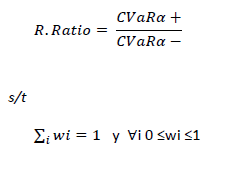
g) Optimización del ratio Omega²⁷

Se trata también de un ratio tipo R/R que se define como la probabilidad de las ganancias obtenidas respecto de las pérdidas a partir de un nivel que se considera como parámetro. Es decir se divide la distribución acumulada del retorno F(x) en dos tramos R < r > R de tal modo que:

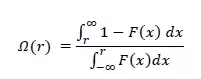
Dónde r es el umbral de rentabilidad mínima exigida para cada operación o período (días, semanas, meses) en la serie de retornos. En muchos casos este parámetro queda fijo, con un valor de r=0.01.

Una de las ventajas²⁸ de balancear con este ratio es que variando el umbral de rentabilidad mínima exigida en cada operación o período en función del ratio podemos conseguir resultados equivalentes a los que se obtienen con otros ratios.

La optimización del ratio Ω es un problema de cómputo no lineal, por tanto las mejores herramientas de optimización para resolver esta tarea son las de tipo estocástico y evolutivo.

h) Optimización del ratio de Calmar²⁹

Este ratio, conocido también como Drawdown Ratio, pertenece a la familia R/R y suele ser muy utilizado por la industria Hedge Fund y gestores alternativos. Se define como el cociente entre el retorno anualizado (AROR) y el DD máximo de un activo:

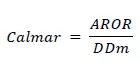
Podemos optimizar un portfolio en términos de DD máximo para un nivel mínimo de rentabilidad esperada o realizar la asignación maximizando directamente el ratio.

(Continuará…)

 

Acerca del autor
Andrés A. García es Doctor en Filosofía, especializado en Lógica y Filosofía de la Ciencia, Doctor en Ciencias de la Educación y Experto en Nuevas Tecnologías. Durante más de 20 años ha compaginado la enseñanza y la operativa por cuenta propia, centrándose en la última década en el desarrollo de algoritmos automáticos de trading en los mercados de futuros estadounidenses y europeos. Es propietario de una de las páginas web más conocidas y visitadas en España sobre trading de sistemas y temas afines: TradingSys.org. También es autor de un libro sobre “Futuros de renta fija y operativa intradiaria” (2009), de numerosos artículos sobre mercados financieros en diversas webs y publicaciones especializadas y ha impartido conferencias en varias universidades. Actualmente es profesor del curso de postgrado «Sistemas y modelos cuantitativos de  trading algorítmico» organizado por la Universidad Politécnica de Madrid. Desde 2010 es cofundador y socio de la empresa Optimal Quant Management, que ofrece formación online avanzada y de alta calidad sobre trading de sistemas. Así mismo es socio y cofundador de la empresa  ATP Capital Management LLC  (2013), un CTA (Commodity Trading Advisor) que opera en EEUU.

 

Referencias

¹ Benjamin B., Koudiraty A., Darolles  y S. Roncalli (2011), “Portfolio Allocation of Hedge Funds”,  Lyxor White Paper (5).
² Markowitz H. (1952), “Portfolio Selection”, Journal of Finance (7) pp. 77-91.
³ Sharpe W. (1963) “A Simplified Model for Portfolio Analysis”, Management Science, (8) pp. 277-293. Véase también (2007):  “Expected Utility Asset Allocation”, Financial Analysts Journal (63) pp. 18-30.
⁴ Adam A., Houkari M. and Laurent J.P. (2008), “Spectral Risk Measures and Portfolio Selection”, Journal of Banking and Finance (32) pp. 1870-1882.
⁵ Buraschi A., Kosowski R. and Trojani F. (2010), “When There Is No Place to Hide: Correlation Risk and the Cross-Section of Hedge Fund Returns”, Review of Financial Studies (27) pp. 581-616.
⁶ J. G. Kallberg y W. T. Ziemba (1983) “Comparison of Alternative Utility Functions in Portfolio Selection Problems”, Management Science, vol. 29, pp. 1257 – 1276.
⁷ Jobson, J.D., and Korkie, B. (1980) “Estimation for Markowitz efficient portfolios”, Journal of the American Statistical Association, Vol. 75, No. 371, pp. 544-554.
⁸ Hirschberger, M., Qi Y. y Steuer R.E. (2008) “Large-Scale MV Efficient Frontier Computation via a Procedure of Parametric Quadratic Programming” Journal Decision Support Systems (51) pp. 250-255.
⁹ H. Letane, “Criteria for Choice Among Risky Ventures”, Journal of Political Economy (1959) pp. 144-155.
¹⁰ Vince, R. (1990) Portfolio Management Formulas: Mathematical Trading Methods for the Futures, Op-tions, and Stock Markets, Wiley & Sons.
¹¹ Latane, H. (1959). “Criteria for Choice Among Risky Ventures.” Journal of Political Economy (67) pp. 144-155.
¹² Breiman, L. (1961). “Optimal Gambling Systems for Favorable Games.” Fourth Berkeley Symposium on Probability and Statistics (1) pp. 65-78.
¹³ Hakansson, N. (1971). “Capital Growth and the Mean-Variance Approach to Portfolio Selection.” Journal of Financial and Quantitative Analysis (6) pp. 517-557.
¹⁴ Aucamp, D. (1993) “On the extensive number of plays to achieve superior performance with the geometric mean strategy”,  Management Science 39 (9) pp. 1163-1172.
¹⁵ Véase por ejemplo: Bernstein, W.  y David W. (1997). “Diversification, Rebalancing, and the Geometric Mean Frontier.” Unpublished manuscript. http://www.effisols.com/basics/rebal.pdf. Estos autores desarrollaron la aplicación MVO Plus (http://effisols.com/mvoplus/index.htm) que puede calcular la frontera eficiente para los modelos MV y GGM y hacer rebalanceos multiperiodo.
¹⁶ Samuelson, P. (1963). “Risk and Uncertainty: A Fallacy of Large Numbers.” Scientia, 1-6.
¹⁷ Markowitz, H.(1959). Portfolio Selection. Efficient Diversification of Investments. John Wiley & Sons.
¹⁸ Roy, A. (1952). Safety first and the holding of assets. Econometrica 20 (3) pp. 431-449.
¹⁹ J. Estrada (2010) “Geometric mean maximization: an overlooked portfolio approach?” Journal of Inves-ting, vol. 19, no. 4, pp. 134–147. Este artículo es una excelente revisión de los modelos MV y GGM, situando el debate entre ambos planteamientos en su perspectiva histórica.
²⁰ SRM son las siglas de Sharpe Ratio Maximization, ya que se puede demostrar formalmente que el portfolio situado en la frontera con mejores propiedades es aquel que maximiza el ratio de Sharpe.
²¹ GMM (Geometric Mean Maximization).
²² Pfaff B. (2016) Financial Risk Modelling and Portfolio Optimisation with R, Wiley, Nueva York.
²³ Sobre este tema véase por ejemplo Patrick Burns y su plataforma: Portfolio Probe. http://www.portfolioprobe.com/about/random-portfolios-in-finance/
²⁴ Bernstein, WJ. and Wilkinson, D., «Diversification, Rebalancing and the Geometric Mean Frontier», research manuscript (November 1997).
²⁵ Choueifaty, Yves, and Yves Coignard. “Toward Maximum Diversification.” Journal of Portfolio Management, Vol. 34, No. 4 (2008), pp. 40–51.
²⁶ Rachev, S., C. Menn, F. Fabozzi (2005) Fat-Tailed and Skewed Asset Return Distributions: Implications for Risk Management, Portfolio Selection, and Option Pricing.  New Jersey: JohnWiley Finance.
²⁷ Keating C. y Shadwick W. (2002) “A Universal Performance Measure”, Finance Development Centre Limited, Londres.
²⁸ Véase mi artículo: “Rebalanceo de carteras sistemáticas y Ratio Omega” (abril 2013) Tradingsys.org.
²⁹ Young T. W. (1991) «Calmar Ratio: A Smoother Tool», Futures Magazine (Oct-1991).

Artículo publicado en el número 29 de 2017 de la revista Hispatrading. Regístrate en www.hispatrading.com de manera completamente gratuita para acceder a más artículos como este.