El sistema matemático de Murrey (Murrey Math Trading System) es un sistema desarrollado por T. Henning Murrey el cual se explica detalladamente en su libro Murrey Math Trading System for All Traded Markets. Se trata de un sistema que presenta ciertas similitudes con la Teoría de Gann, si bien se apoya en el uso de otros elementos tales como fractales, octavas musicales, etc. (Por cierto, el tema de las octavas musicales me recuerda cierta web cuyos analisis utilizaban las octavas musicales y que fue montada por alguien denominado Alquimista, aunque no era el que participa habitualmente en el Foro. Si el autor de esa web nos lee, que nos envie un correo lo antes posible).
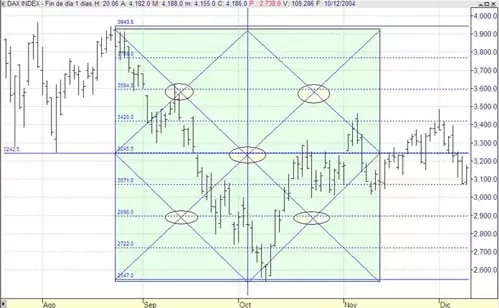
Pero posiblemente las matemáticas de Murrey se entiendan mejor si ilustramos gráficamente de que va todo esto. Básicamente, si observan el gráfico que acompaña este artículo, se trata de calcular el lado de un cuadrado armónico que nos sirva como sistema de referencia tanto espacial (lineas de soporte y resistencia) como temporal (comportamiento cíclico). Asimismo, verán una serie de círculos en el gráfico inferior: dichas áreas son lo que Murrey denomina «zonas de conflicto» y que suelen importantes barreras para el precio.
Sin embargo, la cuestión que ahora mismo estará Vd. preguntándose es: ¿cómo se construye el cuadrado? ¿Es muy complicado? ¿Requiere conocimientos matemáticos muy complejos? En realidad, su construcción es muy sencilla y tan solo requiere seguir una serie de pasos mecánicos. Veamos cómo es dicho proceso.
Calculando cuadrados en el tiempo…
Estos son los pasos a seguir para construir un cuadrado armónico según Murrey:
1. Marcar el ritmo.
Para ello, debemos tomar un máximo y un mínimo recientes en el gráfico que vayamos a estudiar. Normalmente la escala del gráfico será igual a 4 unidades temporales o múltiplos de éste (esto es, 4, 8, 16, 32, 64 días, horas, minutos, etc).
Seguidamente debemos buscar en la escala de ritmo propuesta por Murrey donde cae el máximo seleccionado. Para ello utilizamos la siguiente tabla:
SI (valor maximo del |
Y (valor maximo del |
ENTONCES SR es: |
| 250,000 25,000 2,500 250 25 12.5 6.25 3.125 1.5625 0.390625 |
25,000 2,500 250 25 12.5 6.25 3.125 1.5625 0.390625 0.0 |
100,000 10,000 1,000 100 12.5 12.5 6.25 3.125 1.5625 0.1953125 |
2. ¿En qué octava estamos?
A continuación calculamos el rango en el que se ha movido el activo que estemos analizando, esto es, calculamos Rango = Máximo – Mínimo. Realizamos las siguientes divisiones de forma secuencial:
Rango/(SR/8)
Rango/(SR/8/8)
Rango/(SR/8/8/8)
…
Rango/(SR/8^n)
Donde SR es el valor obtenido en la tabla anterior. En el momento en el que el valor del cociente es mayor o igual a 1.25, debemos parar, siendo el número de ochos empleados el número de octava en el que nos movemos de tal forma que, si por ejemplo hemos obtenido un cociente mayor de 1.25 al calcular Rango/(SR/8/8/8) diremos que estamos en la tercera octava.
3. Determinar la altura y la base del cuadrado
Aqui viene quizás la parte más enrevesada del cálculo por lo que este punto merece una especial atención. Básicamente se trata de lo siguiente:
– Tomamos el valor de SR/8. Dividimos el Mínimo que hemos elegido inicialmente entre esta cantidad; el resultado lo redondeamos a un entero. Seguidamente multiplicamos dicho resultado por SR/8 y se lo sumamos a 0.0 (base ideal del cuadrado armónico).
– El resultado obtenido en el paso anterior se considera ahora la nueva base del cuadrado. Dado que estamos en el segundo paso, tomamos SR/8/8. Asimismo, obtenemos la diferencia entre el Mínimo inicial y el resultado del paso anterior; la dividimos por SR/8/8 y redondeamos el resultado a un número entero. Este entero se multiplica por SR/8/8 y se suma a la cantidad obtenida en el paso anterior.
– Y así sucesivamente hasta que lleguemos al número de octava que corresponda. En ese momento diremos que tenemos un cuadrado de base, la obtenida en este último paso, y de altura el valor redondeado que obtuvimos cuando calculamos Rango/(SR/8^n) multiplicado por 8.
Dado que quizás entender todo esto sin un pequeño ejemplo numérico resulta algo arduo, les propongo el siguiente ejemplo:
Tomamos por ejemplo el futuro del Bund, vencimiento Diciembre 2004. En los últimos días de negociación se aprecia un claro Máximo en 119.28 y un Mínimo en 117.71 puntos. Multiplicando por 100 para eliminar los decimales tenemos que:
Máximo = 11928
Mínimo = 11771
Vamos a la tabla de Murrey y vemos que el máximo cae entre 25000 y 2500, luego SR=10000.
Veamos ahora en qué octava estamos:
Rango = 11928 – 11771 = 157
157 / (SR/8) = 157 / (10000/8) = 157 / 1250 = 0.1256 < 1.25
157 / (10000/8/8) = 157/156.25 = 1.0048 < 1.25
157 / (10000/8/8/8) = 157 / 19.53125 = 8.0384 (aprox. 8)
Luego estamos en la Tercera Octava y la altura del cuadrado es 8.
Finalmente veamos donde está la base del cuadrado.
SR/8 = 1250
Mínimo – 0.0 = 11771
Mínimo / (SR/8) = 11771 / 1250 = 9.4168 (aprox. 9)
0.0 + 9*SR/8 = 11250
Tomamos ahora 11250 como nueva base del cuadrado tal que:
SR/8/8 = 156.25
Mínimo – 11250 = 521
521 / (SR/8/8) = 521 / 156.25 = 3.3344 (aprox. 3)
11250 + 3*SR/8/8 = 11718.75
Terminamos con la tercera octava:
SR/8/8/8 = 19.53125
Mínimo – 11718.75 = 52.25
52.25 / (SR/8/8/8) = 52.25 / 19.53125 = 2.6752 (aprox. 3)
11718.75 + 3*SR/8/8/8 = 11777.34375 (aprox. 11777)
Por tanto, tenemos un cuadrado armónico de base 11777 y altura 8*8 = 64 (o, deshaciendo la transformación, base 117.77 y altura 0.64).
Pero, como se utiliza todo esto para nuestro trading? Cómo se determinan las zonas de conflicto? En la próxima entrega veremos todos estos aspectos en detalle.
X-Trader