En esta tercera entrega, ¡llega el momento que todos estabáis esperando! Pasamos a desarrollar toda una batería de código en Python que nos permitirán analizar y extraer fácilmente patrones estacionales de cualquier serie financiera. Dicho esto, ¡comenzamos!
Extrayendo Patrones Estacionales con el Drawdown
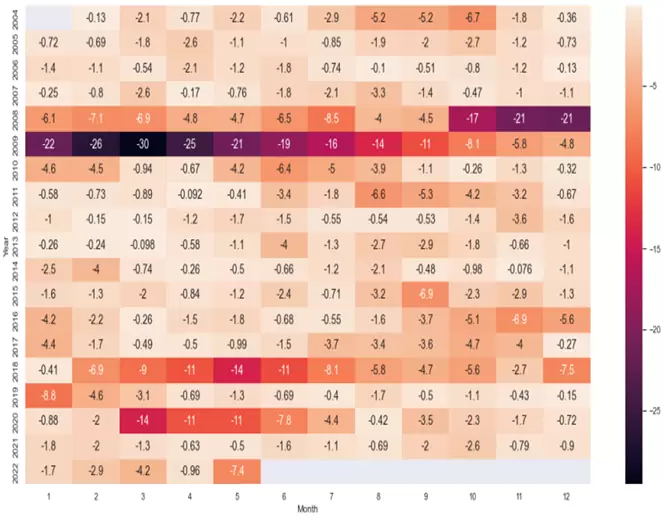
Una primera aproximación que podemos adoptar para buscar patrones estacionales es analizar los drawdowns que se producen en el precio. Para ello, podemos crear una tabla de drawdowns mensuales en forma de mapa de calor utilizando el siguiente código:
# Tabla de Drawdowns mensuales
tabladdm = pd.pivot_table(df, values="drawdown", index="Month", columns="Year")
tabladdm.T
pdd=sns.heatmap(tabladdm.T.iloc[0:22,0:12], annot=True, annot_kws={"size": 14})El resultado obtenido es el siguiente:
También podemos relativizar el resultado comparando el drawdown promedio mensual con el drawdown más alto del mes:
# DD promedio mensual vs DD más alto:
tabladdm_mean = df.groupby("Month").drawdown.mean()
tabladdm_mean = pd.DataFrame(tabladdm_mean)
tabladdm_mean.columns = ["drawdown_mean"]
tabladdm_min=df.groupby("Month").drawdown.min()
tabladdm_min = pd.DataFrame(tabladdm_min)
tabladdm_min.columns = ["drawdown highwest"]
tabladdm_resumen = pd.concat([tabladdm_mean, tabladdm_min], axis=1)
tabladdm_resumen.T
pddm=sns.heatmap(tabladdm_resumen.T.iloc[0:4,0:12], annot=True, annot_kws={"size": 14})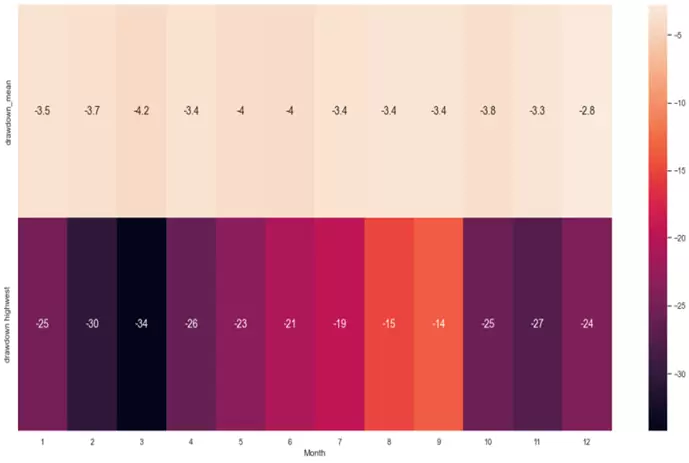
No obstante, podemos hilar más fino, elaborando un mapa de calor que nos permita analizar el drawdown combinando dos dimensiones: mes del año y día del calendario.
# Tabla de Drawdowns por día del calendario.
tabladdd=pd.pivot_table(df,values="drawdown",index="Day_Calendary", columns="Month", fill_value=0, aggfunc=np.mean, margins=True)
tabladdd.columns = ["Enero", "Febrero", "Marzo", "Abril", "Mayo", "Junio", "Julio", "Agosto", "Septiembre", "Octubre", "Noviembre", "Diciembre", "Prom."]
tabladdd = tabladdd.apply(lambda x: round(x,3))
p2=sns.heatmap(tabladdd.T.iloc[0:13,0:32], annot=True, annot_kws={"size": 12})
tabladdd_mean = df.groupby("Day_Calendary").drawdown.mean()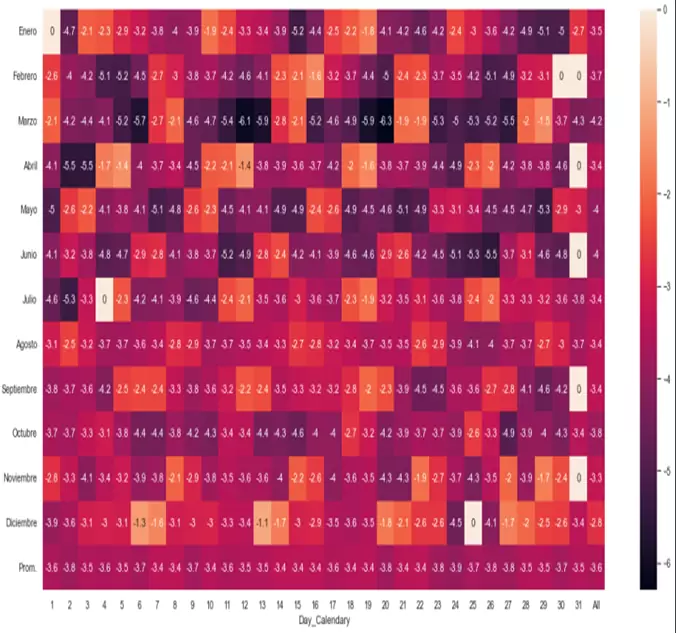
Extrayendo Patrones Estacionales con los Rendimientos
Hasta este momento hemos visto el tema de la estacionalidad desde el punto de vista del drawdown, esto es, de la mayor pérdida producida. Pero también podemos analizarla desde el punto de vista de los rendimientos promedio, usando para ello el siguiente código:
# Tabla de rendimientos promedio mensual.
tablam_acum = pd.pivot_table(df, values="roc1", index="Month", columns="Year", aggfunc=np.sum, margins=True)
tablam = pd.pivot_table(df, values="roc1", index="Month", columns="Year", fill_value=0)
tablam = tablam.apply(lambda x: round(x,3))
tablam.T
p1=sns.heatmap(tablam.T.iloc[0:22,0:12], annot=True, annot_kws={"size": 14})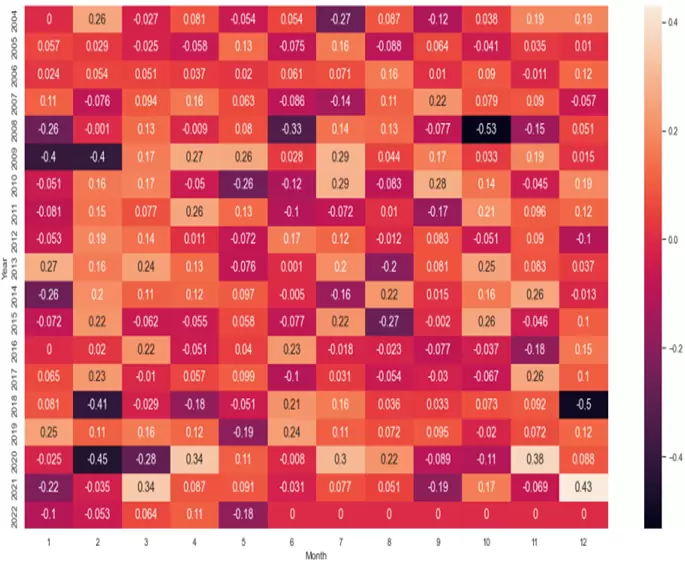
O incluso podemos sacar una tabla que nos resuma los rendimientos promedio por mes y año:
# Tabla Resumen % valores positivos y negativos por mes.
algo=tablam.T.iloc[0:22,0:12]
algo1=pd.DataFrame(algo[algo>0.05].count())
algo2=pd.DataFrame(algo.count())
tablam_pos=pd.DataFrame(algo1/algo2)*100
tablam_resumen = pd.concat([tablam, tablam_pos], axis=1)
tablam_resumen=tablam_resumen.rename(columns={0: "%ValuesPos"})
Y ya puestos, ¿por qué no sacar una tabla que nos resuma por cada mes del año el rendimiento promedio, el rendimiento mínimo, la desviación típica de los rendimientos y el drawdown promedio?
# Tabla resumen general mensual, promedio retorno-mínimo retorno-stdev-DD
tablam_mean = df.groupby("Month").roc1.mean()*100
tablam_mean = pd.DataFrame(tablam_mean)
tablam_mean.columns = ["mean_roc1"]
tablam_min = df.groupby("Month").roc1.min() #tablam_min = tablam.apply(lambda x: min(x))
tablam_min = pd.DataFrame(tablam_min)
tablam_min.columns = ["min_roc1"]
tablam_std = df.groupby("Month").roc1.std()
tablam_std = pd.DataFrame(tablam_std)
tablam_std.columns = ["std_roc1"]
tablam_resumen = pd.concat([tablam_mean, tablam_min, tablam_std, tabladdm_mean], axis=1)
tablam_resumen = tablam_resumen.apply(lambda x: round(x,3))
tablam_resumen.T
prm=sns.heatmap(tablam_resumen.T.iloc[0:4,0:12], annot=True, annot_kws={"size": 14})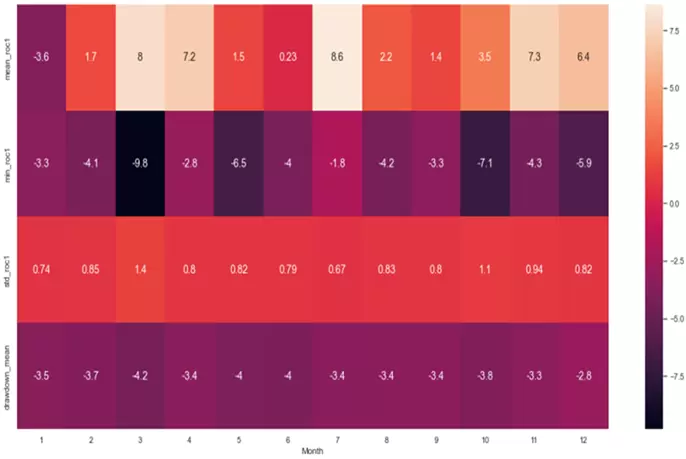
Con toda esta información ya podríamos extraer conclusiones interesantes y útiles para construir estrategias basadas en estacionalidad. Por ejemplo, podemos ver que marzo, abril, julio y noviembre suelen ser meses alcistas en el Vanguard Consumer Staples ETF, aunque marzo y abril tienden a ser volátiles dados sus importantes drawdowns. Asimismo llama la atención como marzo, mayo y octubre suelen ser meses con fuertes rachas bajistas en el ETF.
Veamos ahora un filtrado de rendimientos combinando dos dimensiones: mes del año y día del calendario.
# Tabla de rendimientos diarios
tablad_acum=pd.pivot_table(df,values="roc1",index="Day_Calendary", columns="Month", aggfunc=np.sum,margins=True)
tablad = pd.pivot_table(df, values="roc1", index="Day_Calendary", columns="Month", fill_value=0)
tablad.columns = ["Enero", "Febrero", "Marzo", "Abril", "Mayo", "Junio", "Julio", "Agosto", "Septiembre", "Octubre", "Noviembre", "Diciembre"]
tablad = tablad.apply(lambda x: round(x,2))
p2=sns.heatmap(tablad.T.iloc[0:12,0:31], annot=True, annot_kws={"size": 10})
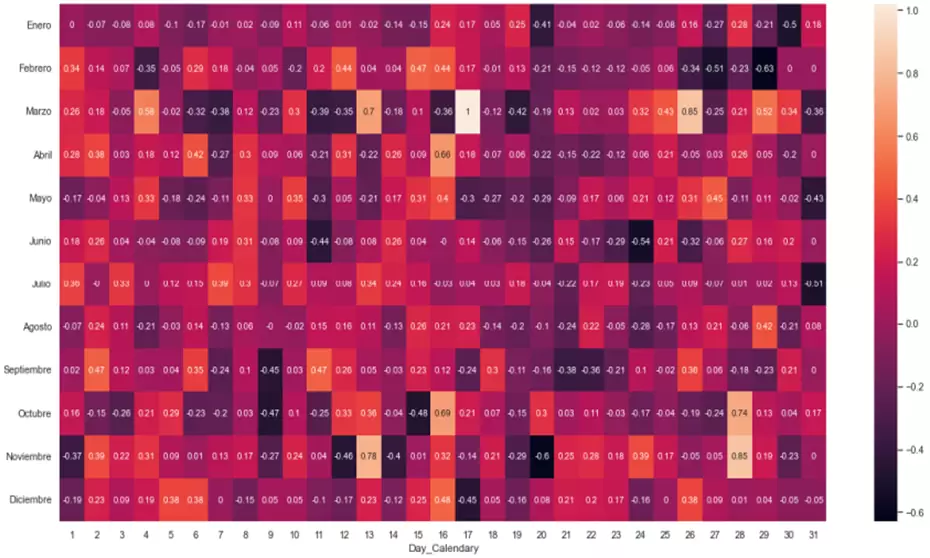
También podemos sacar una tabla con el rendimiento promedio, el rendimiento mínimo, la desviación típica de los rendimientos y el drawdown promedio por día del calendario:
# Tabla resumen % valores positivos y negativos por día calendario.
algo=tablad.T.iloc[0:22,0:31]
algo1=pd.DataFrame(algo[algo>0.05].count())
algo2=pd.DataFrame(algo.count())
tablad_pos=pd.DataFrame(algo1/algo2)*100
tablad_resumen = pd.concat([tablad, tablad_pos], axis=1)
tablad_resumen=tablad_resumen.rename(columns={0: "%ValuesPos"})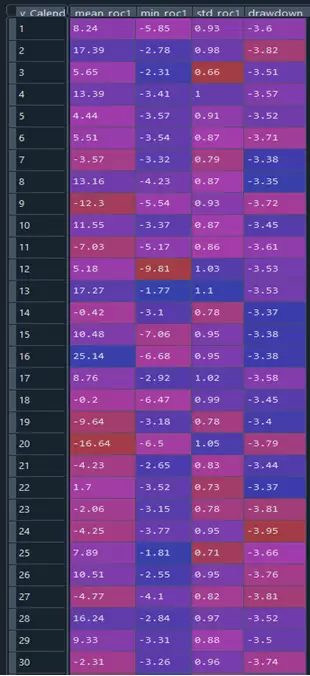
Hasta el momento hemos trabajado con días del calendario, pero ¿habrá algo interesante en el nº de la semana de cada mes? Analicémoslo:
# Tabla de rendimientos semanales
tablasem_acum = pd.pivot_table(df2, values="roc1", index="W_of_M", columns="Month", aggfunc=np.sum,margins=True)
tablasem = pd.pivot_table(df2, values="roc1", index="W_of_M", columns="Month", fill_value=0)
tablasem.columns = ["Enero", "Febrero", "Marzo", "Abril", "Mayo", "Junio", "Julio", "Agosto", "Septiembre", "Octubre", "Noviembre", "Diciembre"]
tablasem = tablasem.apply(lambda x: round(x,2))
psem = sns.heatmap(tablasem.T.iloc[0:12,0:5], annot=True, annot_kws={"size": 14})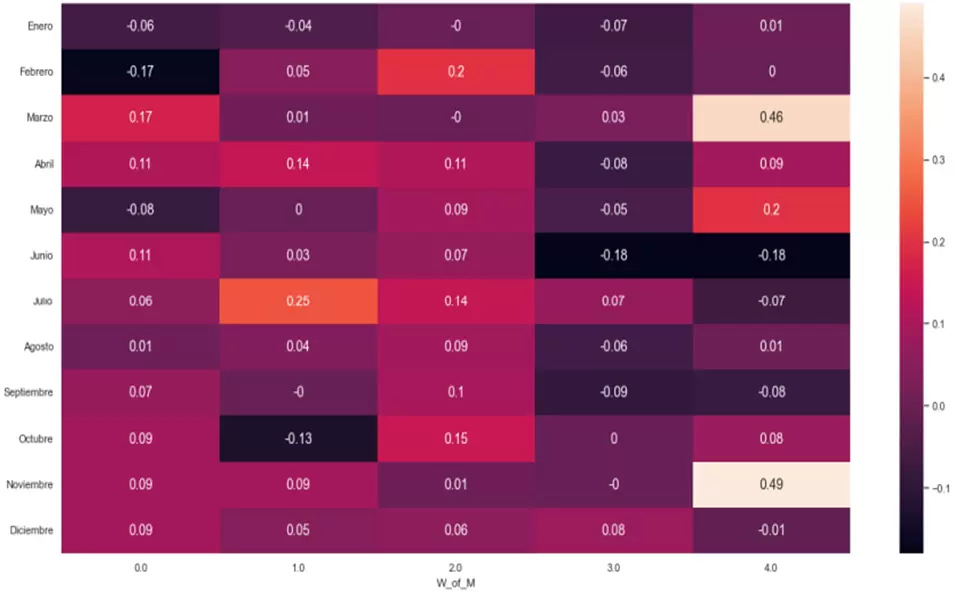
Resultan especialmente llamativas por su rendimiento promedio, tanto la subida en la última semana de marzo y de noviembre, como las bajadas en la primera semana de febrero, en las dos últimas semanas de junio, y en la segunda semana de octubre.
Combinamos ahora nº de la semana con meses para examinar el rendimiento promedio:
# Tabla resumen % valores positivos y negativos por número de la semana del mes.
algosem = tablasem.T.iloc[0:22,0:5]
algosem1 = pd.DataFrame(algosem[algosem>0.05].count())
algosem2 = pd.DataFrame(algosem.count())
tablasem_pos = pd.DataFrame(algosem1/algosem2)*100
tablasem_resumen = pd.concat([tablasem, tablasem_pos], axis=1)
tablasem_resumen = tablasem_resumen.rename(columns={0: "%ValuesPos"})
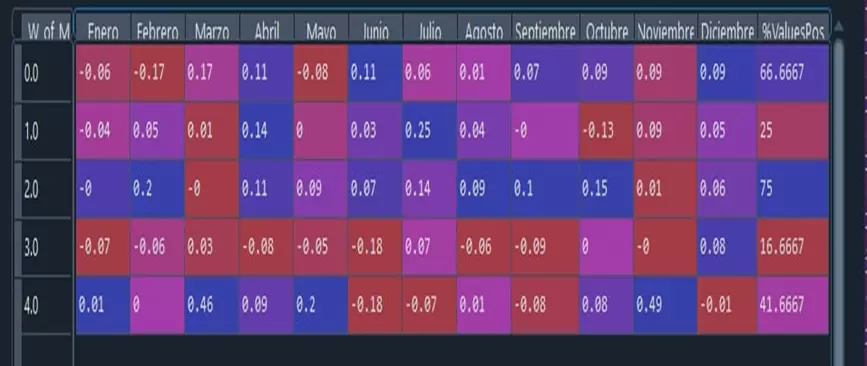
Por último, para obtener más información generamos una tabla con el rendimiento promedio, el rendimiento mínimo, la desviación típica de los rendimientos y el drawdown promedio por número de la semana:
# Tabla resumen general semanal, promedio retorno-mínimo retorno-stdev-DD
tablasem_mean = df2.groupby("W_of_M").roc1.mean()*100
tablasem_mean = pd.DataFrame(tablasem_mean)
tablasem_mean.columns = ["mean_roc1"]
tablasem_min = df2.groupby("W_of_M").roc1.min() #tablam_min = tablam.apply(lambda x: min(x))
tablasem_min = pd.DataFrame(tablasem_min)
tablasem_min.columns = ["min_roc1"]
tablasem_std = df2.groupby("W_of_M").roc1.std()
tablasem_std = pd.DataFrame(tablasem_std)
tablasem_std.columns = ["std_roc1"]
tablasem_resumen=pd.concat([tablasem_mean, tablasem_min, tablasem_std, tabladdd_mean], axis=1)
tablasem_resumen = tablasem_resumen.apply(lambda x: round(x,2))
tablasem_resumen.T
psemr = sns.heatmap(tablasem_resumen.T.iloc[0:4,0:5], annot=True, annot_kws={"size": 14})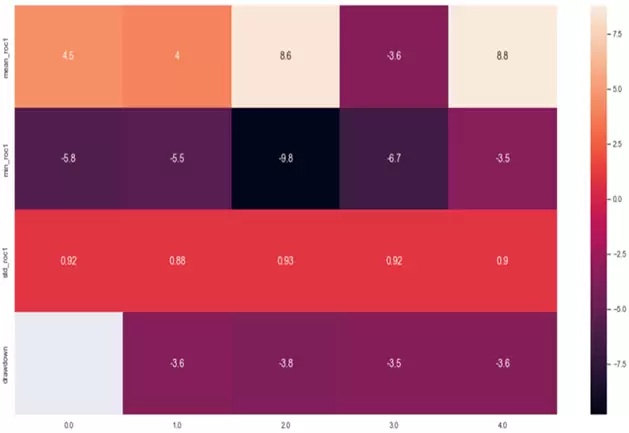
Podemos también repetir el análisis anterior pero en lugar de trabajar con el número de la semana dentro de cada mes, utilizamos el número de semana en el año. A continuación podéis ver el código, similar al de los casos anteriores, así como los resultados obtenidos:
# Tabla de rendimientos por número de la semana del año.
tablasem2_acum = pd.pivot_table(df, values="roc1", index="Week", columns="Year", aggfunc=np.sum,margins=True)
tablasem2=pd.pivot_table(df2,values="roc1",index="Week",columns="Month", fill_value=0)
tablasem2.columns = ["Enero", "Febrero", "Marzo", "Abril", "Mayo", "Junio", "Julio", "Agosto", "Septiembre", "Octubre", "Noviembre", "Diciembre"]
tablasem2 = tablasem2.apply(lambda x: round(x,2))
# Tabla resumen % valores positivos y negativos por número de la semana del año.
algosem2 = tablasem2.T.iloc[0:22,0:52]
algosem22 = pd.DataFrame(algosem2[algosem2>0.05].count())
algosem22 = pd.DataFrame(algosem.count())
tablasem2_pos = pd.DataFrame(algosem21/algosem22)*100
tablasem2_resumen = pd.concat([tablasem2, tablasem2_pos], axis=1)
tablasem2_resumen = tablasem2_resumen.rename(columns={0: "%ValuesPos"})
# Tabla resumen general por número de la semana del año, promedio retorno-mínimo retorno-stdev-DD.
tablasem2_mean = df2.groupby("Week").roc1.mean()*100
tablasem2_mean = pd.DataFrame(tablasem2_mean)
tablasem2_mean.columns = ["mean_roc1"]
tablasem2_min = df2.groupby("Week").roc1.min() #tablam_min = tablam.apply(lambda x: min(x))
tablasem2_min = pd.DataFrame(tablasem2_min)
tablasem2_min.columns = ["min_roc1"]
tablasem2_std = df2.groupby("Week").roc1.std()
tablasem2_std = pd.DataFrame(tablasem2_std)
tablasem2_std.columns = ["std_roc1"]
tablasem2_resumen = pd.concat([tablasem2_mean, tablasem2_min, tablasem2_std, tabladdd_mean], axis=1)
tablasem2_resumen = tablasem2_resumen.apply(lambda x: round(x,2))
tablasem2_resumen.T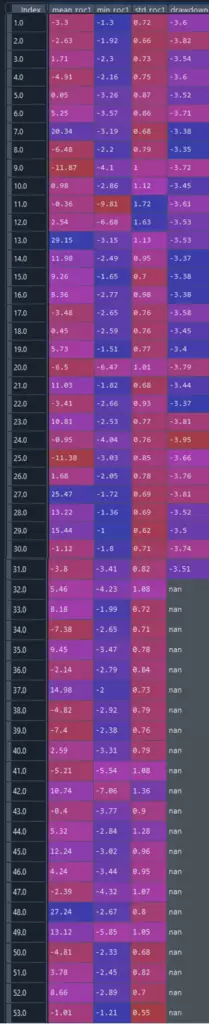
Otra cosa que podemos hacer y que puede resultarnos muy interesante es filtrar valores positivos o negativos superiores o inferiores a una determinada cuantía. Por ejemplo, podemos sacar los rendimientos promedio superiores al +10% o inferiores al -10%, clasificándolos por mes y día del calendario:
# Filtrado de retornos positivos.
tablad_filter_pos = tablad[tablad[0:31] > 0.1] #Retornos positivos de todo el dataframe "tablad_roc1"
count = tablad_filter_pos.count()
print(count)
# Filtrado de retornos negativos
tablad_filter_neg = tablad[tablad[0:31] < -0.1] #Retornos negativos de todo el dataframe "tablad_roc1"
count = tablad_filter_neg.count()
print(count)Los resultados que se obtienen en forma de tabla son los siguientes:
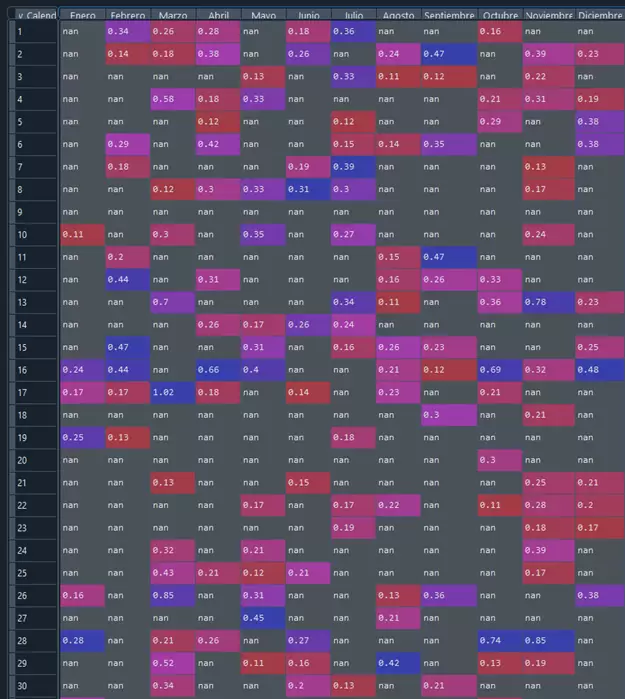
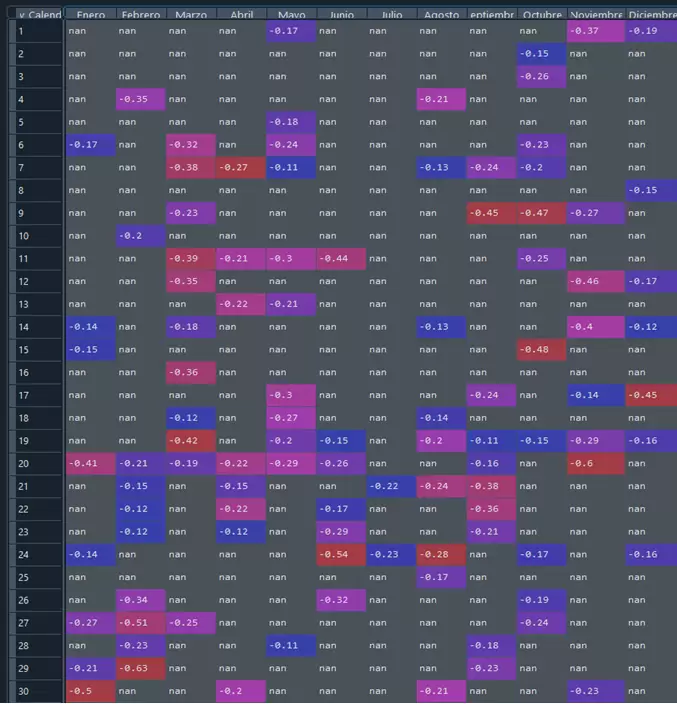
Las tablas anteriores quedan más estéticas si quitamos los NaN que aparecen:
# Filtramos los retornos positivos eliminando además los NAs
tablad_filter_pos_enero = tablad_filter_pos["Enero"].dropna()
tablad_filter_pos_febrero = tablad_filter_pos["Febrero"].dropna()
tablad_filter_pos_marzo = tablad_filter_pos["Marzo"].dropna()
tablad_filter_pos_abril = tablad_filter_pos["Abril"].dropna()
tablad_filter_pos_mayo = tablad_filter_pos["Mayo"].dropna()
tablad_filter_pos_junio = tablad_filter_pos["Junio"].dropna()
tablad_filter_pos_julio = tablad_filter_pos["Julio"].dropna()
tablad_filter_pos_agosto = tablad_filter_pos["Agosto"].dropna()
tablad_filter_pos_septiembre = tablad_filter_pos["Septiembre"].dropna()
tablad_filter_pos_octubre = tablad_filter_pos["Octubre"].dropna()
tablad_filter_pos_noviembre = tablad_filter_pos["Noviembre"].dropna()
tablad_filter_pos_diciembre = tablad_filter_pos["Diciembre"].dropna()
# Filtramos los retornos negativos eliminando además los NAs
tablad_filter_neg_enero = tablad_filter_neg["Enero"].dropna()
tablad_filter_neg_febrero = tablad_filter_neg["Febrero"].dropna()
tablad_filter_neg_marzo = tablad_filter_neg["Marzo"].dropna()
tablad_filter_neg_abril = tablad_filter_neg["Abril"].dropna()
tablad_filter_neg_mayo = tablad_filter_neg["Mayo"].dropna()
tablad_filter_neg_junio = tablad_filter_neg["Junio"].dropna()
tablad_filter_neg_julio = tablad_filter_neg["Julio"].dropna()
tablad_filter_neg_agosto = tablad_filter_neg["Agosto"].dropna()
tablad_filter_neg_septiembre = tablad_filter_neg["Septiembre"].dropna()
tablad_filter_neg_octubre = tablad_filter_neg["Octubre"].dropna()
tablad_filter_neg_noviembre = tablad_filter_neg["Noviembre"].dropna()
tablad_filter_neg_diciembre = tablad_filter_neg["Diciembre"].dropna()El resultado que obtenemos es el siguiente:

Por supuesto, nada nos impide graficar los rendimientos promedio de cada mes, la desviación estándar promedio diaria y mostrar un mapa de calor con los rendimientos promedio diarios de cada día del calendario para poder detectar visualmente pautas en el comportamiento estacional del ETF:
# Retornos medios de cada mes, la desviación estándar promedio diario y mapa de calor de los retornos promedio por día del mes.
fig,(ax1, ax2, ax3) = plt.subplots(3, 1, sharex=False, figsize=(24, 14), gridspec_kw = {"height_ratios":[4, 2, 1]})
fig.suptitle(caso_heatmap_principal)
sns.heatmap(tablad, annot = True, annot_kws={"size": 11}, vmin=0, vmax=0.5, cmap = "Greens", cbar = False, ax=ax1)
ax1.axes.xaxis.set_label_text("")
ax2.set_title("% Retornos medios por mes")
tablam_mean.plot.bar(ax=ax2, color={"blue"})
ax2.axes.xaxis.set_label_text("")
ax3.set_title("Promedio Desviación Estándar diaria")
tablad_std.plot.bar(ax=ax3,color={"orange"})
plt.show()
Otra representación visual que nos puede venir muy bien es crear gráficos de línea para cada mes mostrando el rendimiento promedio de cada uno de los días que lo componen:
# Ploteamos retornos promedio diario de cada mes
ax= plt.axes([0.8, 0.8, 0.8, 0.8])
ax.set_xlim(1,31)
ax.xaxis.set_major_locator(plt.MultipleLocator(1.0))
ax.xaxis.set_minor_locator(plt.MultipleLocator(1.0))
ax.yaxis.set_major_locator(plt.MultipleLocator(0.1))
ax.yaxis.set_minor_locator(plt.MultipleLocator(1.0))
tablad.cumsum().plot(figsize=(14,8), title = caso_roc_general, legend ="Meses")
plt.xlabel("Días del Calendario")
plt.ylabel("Puntos Porcentual de Rendimientos")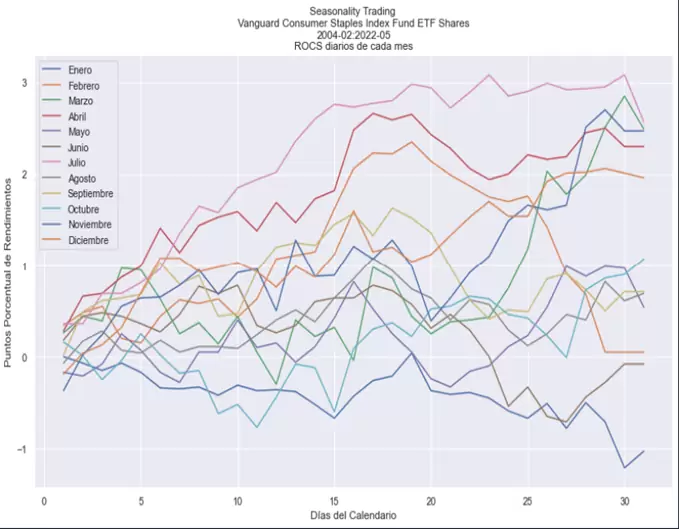
Por supuesto, podemos extraer cada curva de forma individual con el siguiente código (basta con cambiar el nombre del mes en la antepenúltima fila):
ax = plt.axes([0.8, 0.8, 0.8, 0.8]);
ax.set_xlim(1,31);
ax.xaxis.set_major_locator(plt.MultipleLocator(1.0))
ax.xaxis.set_minor_locator(plt.MultipleLocator(1.0))
ax.yaxis.set_major_locator(plt.MultipleLocator(0.1))
ax.yaxis.set_minor_locator(plt.MultipleLocator(1.0))
tablad["Enero"].cumsum().plot(figsize=(14,8), title = caso_roc_individual, color = "red", legend ="Enero")
plt.xlabel("Días del Calendario")
plt.ylabel("Puntos Porcentual de Rendimientos")El resultado de las curvas individuales para cada mes sería el siguiente:
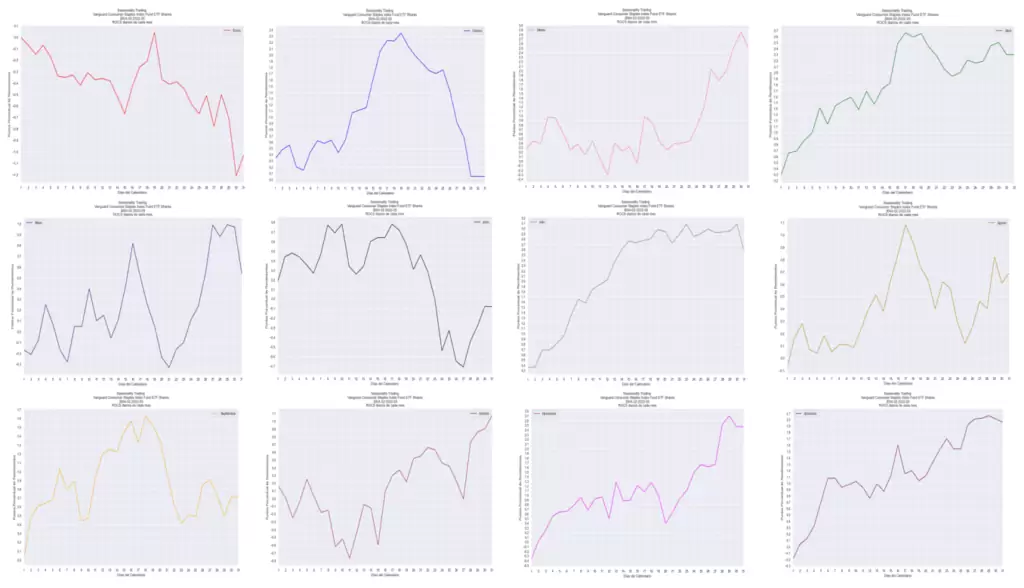
Selección de Días en Base al Ratio de Sharpe
Para terminar, podemos dar mayor validez a los resultados estableciendo un criterio para seleccionar los días cuya pauta es realmente significativa. Por ejemplo, podemos dividir los meses en tres decenas y utilizar el ratio de Sharpe para decidir en qué casos el rendimiento promedio es realmente significativo:
# Calculamos Ratio de Sharpe.
# Función para calcular el ratio de Sharpe
def annualised_sharpe(returns, N=252):
'''
Calcula el ratio Sharpe de una serie
'''
if returns.sum()==0: return 0
return np.sqrt(N) * (returns.mean() / returns.std())
###########################################################
#Sharpe por meses
meses=[]
res=np.zeros(12)
for n in range(1,13):
sharpecat=np.where((df.Month==n),1,0)
sharpe=annualised_sharpe(sharpecat*df.roc1)
print (" El sharpe del mes ", n, " es del orden de ", sharpe)
res[n-1]=sharpe
print
meses.append(res)
mesenas=pd.DataFrame(meses,columns=["1","2","3","4","5","6","7","8","9","10","11","12"])
mesenas.T
mesenas1=pd.DataFrame(mesenas.T)
#mesenas = pd.DataFrame.transpose(mesenas)
#mesenas.columns = ["ratio sharpe"]
ps=sns.heatmap(mesenas, annot=True, annot_kws={"size": 14})
#Criterio de selección de días
#Vamos a seleccionar los meses por Decenas y ver su comportamiento.
# Primera Decena
meses=[ ]
res=np.zeros(12)
for n in range(1,13):
sharpecat=np.where((df.Month==n)&(df.Day_Calendary>0)&(df.Day_Calendary<=10),1,0)
sharpe=annualised_sharpe(sharpecat*df.roc1)
print ("El sharpe del mes", n, "Es del orden de", sharpe)
res[n-1]=sharpe
print
meses.append(res)
# Segunda Decena
res=np.zeros(12)
for n in range(1,13):
sharpecat=np.where((df.Month==n)&(df.Day_Calendary>10)&(df.Day_Calendary<=20),1,0)
sharpe=annualised_sharpe(sharpecat*df.roc1)
print ("El sharpe del mes", n, "Es del orden de", sharpe)
res[n-1]=sharpe
print
meses.append(res)
# Tercera Decena
res=np.zeros(12)
for n in range(1,13):
sharpecat=np.where((df.Month==n)&(df.Day_Calendary>20)&(df.Day_Calendary<32),1,0)
sharpe=annualised_sharpe(sharpecat*df.roc1)
print ("El sharpe del mes", n, "Es del orden de", sharpe)
res[n-1]=sharpe
print
meses.append(res)
#Resultados por Decenas
decenas=pd.DataFrame(meses,columns=['1','2','3','4','5','6','7','8','9','10','11','12'])
p1=sns.heatmap(decenas, annot=True, annot_kws={"size": 14})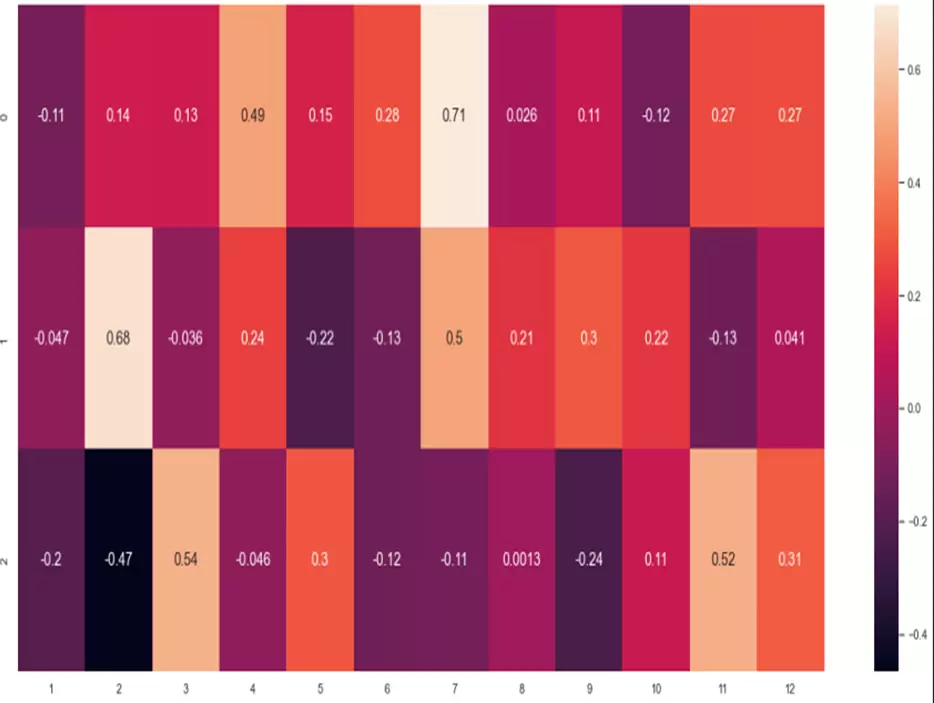
Del mapa de calor anterior podemos destacar algunos resultados: por ejemplo, la tercera decena de febrero es claramente bajista, mientras que la segunda decena de febrero o la primera decena de julio son fuertemente alcistas.
Construyendo la Estrategia
Tras finalizar esta serie de artículos, ahora querido lector dispone de todas las herramientas para caracterizar y construir estrategias de trading basadas en pautas estacionales. Por ejemplo, es posible crear un setup de swing trading que cumpla los siguientes requisitos:
t-test > 0,05
Mediana >= 0,05% Roc
Media >= 0,01% Roc
Sharpe >= 0,55
Roc_mean >= 0,5% and
Roc_mean > Roc_min and
Diff Roc >= 1,05 “Roc_mean/Roc_min”
Desvest <= Desvest. prom. Diario del activo
Por supuesto, les animo a que jueguen con el código proporcionado y que compartan sus resultados, tanto en el Foro de Python de X-Trader como en el canal de Telegram de VTAlgo.