Cointegra… qué???
Pues sí, es probable que salvo que haya estudiado Econometría o Análisis de Series Temporales Vd. nunca haya oído hablar de este término. Pero para poder definir qué es exactamente la cointegración, previamente debemos explicar qué es la integración en el sentido de las series temporales.
Matemáticamente, se dice una serie temporal es integrada de orden d (denotado por I(d)), si después de tomar d diferencias, la serie se convierte en estacionaria; es decir, que una serie será integrada si tomando diferencias entre sus valores logramos que la serie resultante tenga una distribución de probabilidad constante en todos los instantes de tiempo, siendo su media y su varianza fijas.
Por ejemplo, podemos tener una serie cuya media y varianza varían en el tiempo continuamente (por ejemplo el logaritmo de las cotizaciones de Telefónica), por lo que no sería estacionaria, y sin embargo, tomando una diferencia en dicha serie (es decir, calculando lo que gana o pierde el valor con respecto a la sesión anterior en forma de rendimientos logarítmicos) obtengamos otra que oscila en torno a cero y que nunca va más allá de +/-10%, por lo que sería estacionaria. Es decir, habríamos tomado una diferencia por lo que la serie de rendimientos de Telefónica es integrada de orden 1 o, simplemente, I(1).
Por si acaso no queda claro el concepto, las siguientes gráficas seguramente terminen de aclarar el concepto:

Muy bien, ahora que ya sabemos qué es una serie integrada, pasamos a resolver el misterio: ¿qué es la cointegración? Muy sencillo: supongamos que dos series temporales, xt e yt, son estacionarias de orden 1 (es decir, son I(1); para órdenes superiores de integración como I(2), I(3), etc. el problema se complicaría algo más). Se dice que dichas variables están cointegradas cuando puede practicarse una regresión lineal del siguiente tipo:
yt = a·xt + ut
De tal forma que los residuos (errores de ajuste) de la regresión, ut = yt – a·xt sean I(0), esto es, estacionarios. Por tanto, en su versión más sencilla, la cointegración exige que se verifiquen dos condiciones básicas:
- Que dos variables sean integradas de orden 1.
- Que exista una combinación lineal de ambas que sea estacionaria de orden 0.
El concepto de cointegración es relativamente reciente. Fue acuñado en 1987 por C.W.J. Granger, reconocido economista británico que falleció el año pasado y que fue premio Nobel de Economía en 2003 junto con su inseparable compañero Robert Engle (sí, el mismo de los modelos ARCH). En sus investigaciones, Granger observó que la mayoría de los economistas utilizaban series no integradas para estimar relaciones entre ellas, lo cual podía conducir a obtener relaciones espurias, es decir, que se diera el caso de que dos variables estuvieran aparentemente relacionadas cuando en realidad no lo estaban, existiendo una tercera variable desconocida que las relacionaba. Tal sería el caso por ejemplo de un investigador que detecta una relación entre estatura e inteligencia en un colegio. No es que por ser más alto un niño sea más inteligente, sino que al ser más maduros los niños de mayor edad (y, por tanto, mayor estatura) las habilidades y destrezas cognitivas también son mayores. Pues bien, cuando las variables estaban cointegradas este problema desaparece ya que los residuos obtenidos son I(0) indicando que no queda ninguna estructura pendiente de modelizar.
Muy bien pero, ¿qué tiene que ver todo esto con el trading?
Quizás no resulte muy evidente aún pero mediante la cointegración puede ser aplicada al diseño de spreads y coberturas, pudiendo utilizar el parámetro a de la regresión anterior para determinar cuál es la proporción óptima de cada una de las «patas» que utilizaremos para construir un activo cuyas propiedades serán similares a las de una serie I(0). Hasta el momento muchos pensábamos que la determinación de la cantidad de acciones o contratos para cada una de las patas del spread se realizaba en base a dos factores: por un lado, la correlación entre activos, para definir el sentido de las patas; por otro, la volatilidad de cada uno de ellos. Pues bien, el concepto de cointegración nos permite superar el problema de tener que determinar por separado cada una de esas relaciones.
Claro que podríamos preguntarnos por qué no sirve el método tradicional de la correlación. El motivo es sencillo: aparte de las deficiencias estadísticas que presenta el coeficiente de correlación, en el caso de su aplicación al trading el problema es que no siempre nos va a permitir definir relaciones entre variables que sean estacionarias (que, al fin y al cabo, es lo que nos interesa cuando diseñamos un spread). El siguiente ejemplo extraído del blog de Ernest Chan, autor del altamente recomendable Quantitative Trading: How to Build Your Own Algorithmic Trading Business, seguramente les aclare mejor cuál es el problema.
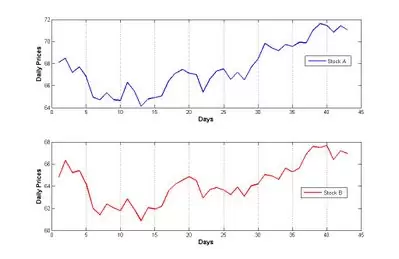
El siguiente gráfico muestra el comportamiento de dos valores, A y B. Como puede observarse ambos están claramente correlacionados, moviéndose a la par:
Sin embargo en este otro en el que se ha superpuesto el comportamiento de los valores A y C, vemos que no existe correlación alguna; sin embargo haciendo el correspondiente test estadístico se comprueba que están cointegrados:
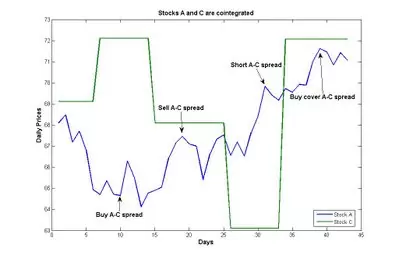
Pues bien, en el caso de los valores correlacionados si calculamos su diferencia podría suceder que, en algunos casos, el resultado también mostrara una clara tendencia o que, por el contrario, no fuese operativo porque el diferencial fuera nulo o demasiado pequeño. Sin embargo, en el caso de los pares de valores cointegrados generalmente calculando su diferencia, el resultado oscilará en torno a un valor de equilibrio de largo plazo que es su media, es decir, es estacionario.
Vale, ahora quiero ganar dinero con esto
Muy bien, pero ojo, que nadie ha dicho que sea sencillo. De hecho deberá analizar bastantes pares de valores hasta que empiece a encontrar algunos que estén cointegrados. Para ello deberá utilizar paquetes estadísticos avanzados que le permitan analizar rápidamente cientos de pares en busca de la tan preciada cointegración. Lo ideal es utilizar Matlab en conjunción con la toolbox gratuita desarrollada por James P. LeSage de la Universidad de Toledo (Ohio). Si no tiene acceso a Matlab o no quiere gastarse dinero siempre puede utilizar la alternativa gratuita a Matlab, R, junto con el paquete URCA para realizar tests de cointegración y disponible en http://cran.r-project.org/web/packages/urca/index.html. Otra alternativa intermedia aunque quizás menos potente es EViews.
Para determinar previamente si cada una de las series que aparecerá en la relación de cointegración es estacionaria podemos utilizar tests como el de Dickey-Fuller, Dickey Fuller Aumentado o Phillips-Perron. Seguidamente deberemos estimar la relación de cointegración por Mínimos Cuadrados Ordinarios y validar la relación, utilizando generalmente para ello el método en dos pasos de Engle y Granger, aunque existen otros métodos como el de Johansen o el de Phillips-Ouliaris. El coeficiente de la relación de cointegración así obtenida nos indicará las proporciones de cada activo en el spread necesarias para obtener un comportamiento estacionario. Una vez obtenido el resultado deseado, obtener señales de compra y venta será tan sencillo como:
- Comprar cuando el spread caiga por debajo de -2 desviaciones típicas con respecto a la media.
- Vender cuando el spread suba por encima de +2 desviaciones típicas con respecto a la media.
Dado que el comportamiento esperado es estacionario, el valor del spread siempre deberá volver al equilibrio, es decir, a la media.
Muy bonito todo, pero ¿y si cambia el comportamiento de las series?
No hay problema porque en esta metodología lo tenemos todo controlado :). Mediante la utilización de lo que se conoce como Modelo de Corrección del Error podemos relacionar el comportamiento a corto plazo de los valores que componen el spread con su comportamiento a largo plazo. Debemos tener en cuenta que una relación de cointegración expresa una relación de equilibrio a largo plazo pero lógicamente en el corto plazo pueden producirse desequilibrios. La forma más sencilla de expresar el Modelo de Corrección del Error sería:
dyt = a·dxt + b·ut-1+et
Donde d indica que se ha aplicado una diferencia a las variables xt,yt y ut-1 son los residuos de la relación de cointegración en el periodo anterior, siendo el parámetro b el responsable de ajustar la relación de corto plazo para que tienda al equilibrio; cuanto más cerca esté b de 1, más rápido volverá al equilibrio el modelo. Por supuesto el modelo se puede complicar y ampliar todo lo que deseemos introduciendo retardos de las variables para mejorar el nivel de ajuste, aunque normalmente no nos interesará tanto saber cómo se tiende al equilibrio sino que las relaciones de cointegración de largo plazo no cambien en el tiempo. Por ello, puede ser una buena idea estimar de nuevo la relación de cointegración entre los valores regularmente para adaptarla a posibles cambios de comportamiento estructural del mercado.
Conclusión
Con la aplicación de la cointegración al campo del diseño de spreads se abre todo un nuevo abanico de posibilidades para el trader, que puede superar los escollos del análisis técnico y del análisis fundamental, construyendo relaciones estadísticas que sean sencillas de operar. Sin embargo, el trabajo no es sencillo y detectar relaciones de cointegración entre activos del mercado puede llevar bastante tiempo; pero posiblemente la relación entre el beneficio potencial y el coste de tiempo y esfuerzo que dediquemos merezca la pena. En próximas entregas, trataremos de mostrar algunos ejemplos.
Saludos,
X-Trader
Lecturas Recomendadas
Alexander, C. (1999), Correlation and Cointegration in Energy Markets en Managing Energy Price Risk (2ª Edición), RISK Publications, pág. 291-304.
Alexander, C. (1999), Optimal Hedging using Cointegration, Philosophical Transactions of the Royal Society, Series A 357 pág. 2039 – 2058.
Granger C. y Engle, R. (1987), «Co-integration and Error Correction: Representation, Estimation and Testing», Econometrica 55(2): pág. 251-276.
Chan, E. (2008), Quantitative Trading: How to Build Your Own Algorithmic Trading Business, Wiley Finance
Montero, R. (2007), «Variables No Estacionarias y Cointegración», Universidad de Granada. Disponible en http://www.ugr.es/~montero/matematicas/cointegracion.pdf